The most heavy chain rule defect: your main chain I am the master

In the last issue , we talked about ways to prevent new honest transactions from being confirmed by “balanced attacks” on the most heavy chain rules.

In this issue, we will talk about another attack method, which we call " segmentation attack . " This type of attack has not been publicly mentioned elsewhere, and was discovered by Conflux when analyzing the security of the "heavy chain rule."

When we introduced the balance attack in the previous issue, we mentioned that the attacker splits the honest node into two equally-powered communities, and uses its control over the network to make the honest nodes of the two communities under different subtrees. Dig a new block to create two subtrees that are roughly the same size.

The attack method described in this issue is similar to the balanced attack at the beginning. It also divides the honest node into several communities with similar computing power. Each community digs blocks under different subtrees. Here we take the example of splitting into three communities.

• Getting started with blockchain | Hash lock for cross-chain technology solutions
• Technical Perspectives | How much does the Python Smart Contract Execution API know?
• Comparison of IPFS and EdgeFS for Secure Edge/IoT Computing Use Cases

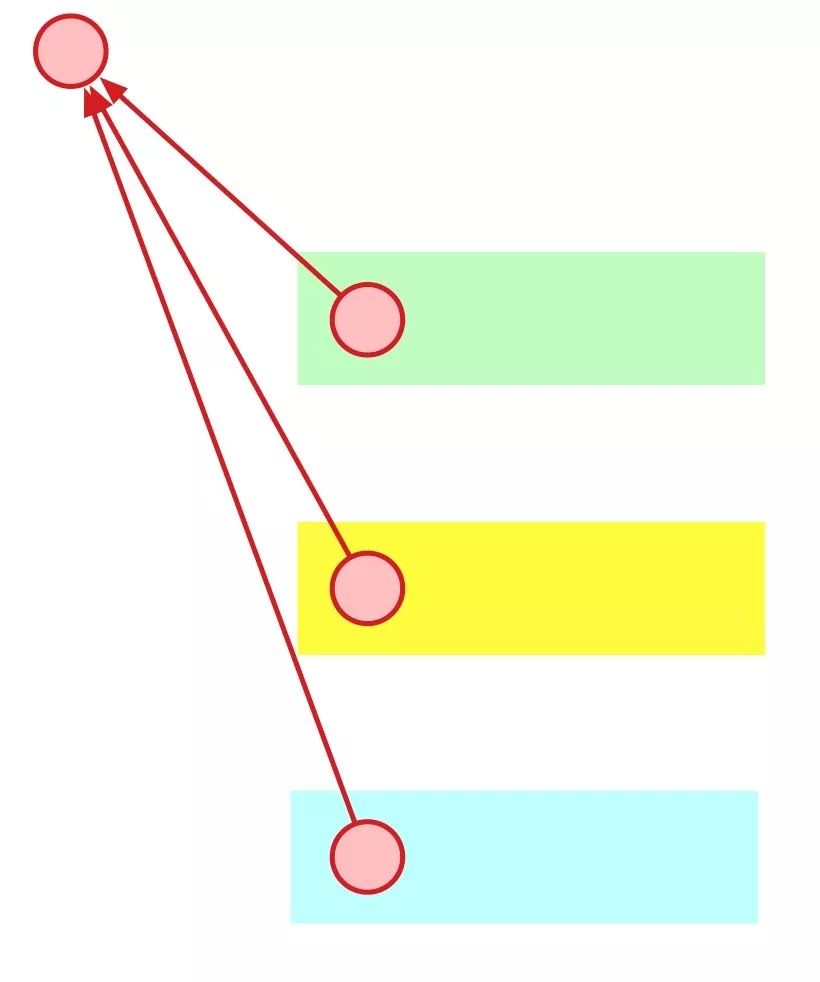
(Each red circle in the figure represents a block, and the attacker lets the honesty nodes of the three communities contribute computing power under the three different subtrees on the right side)

At the same time, the attacker will generate a block behind the father block of the three blocks (the circle on the upper left side in the figure above) and dig a block below the block. After a while, the structure between the blocks is shown below. (Here we assume that the attacker accounts for 40% of the total network.)

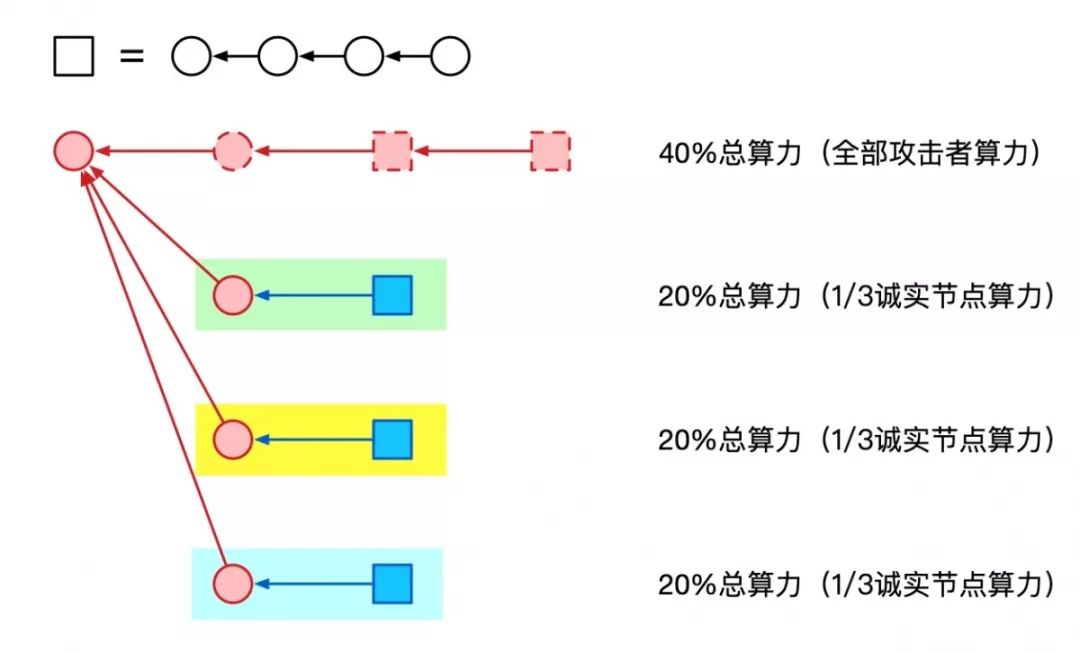
(The box in the figure represents some newly generated blocks over a period of time. The dotted line indicates that the bad guy is hiding and there is no broadcast block. The blue color indicates the block generated by the good person.)

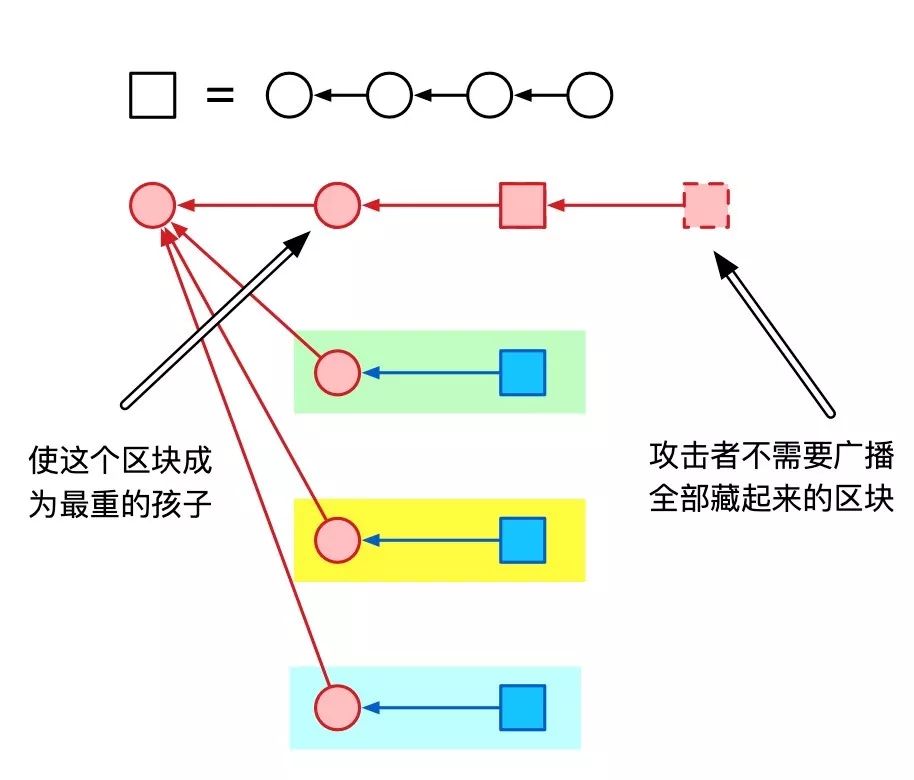
Unlike a balanced attack, the attacker does not intend to let the three good people's communities fight for the three subtrees. Instead, the attacker made the previously hidden child the heaviest child.

After that, the attacker repeats the above process.

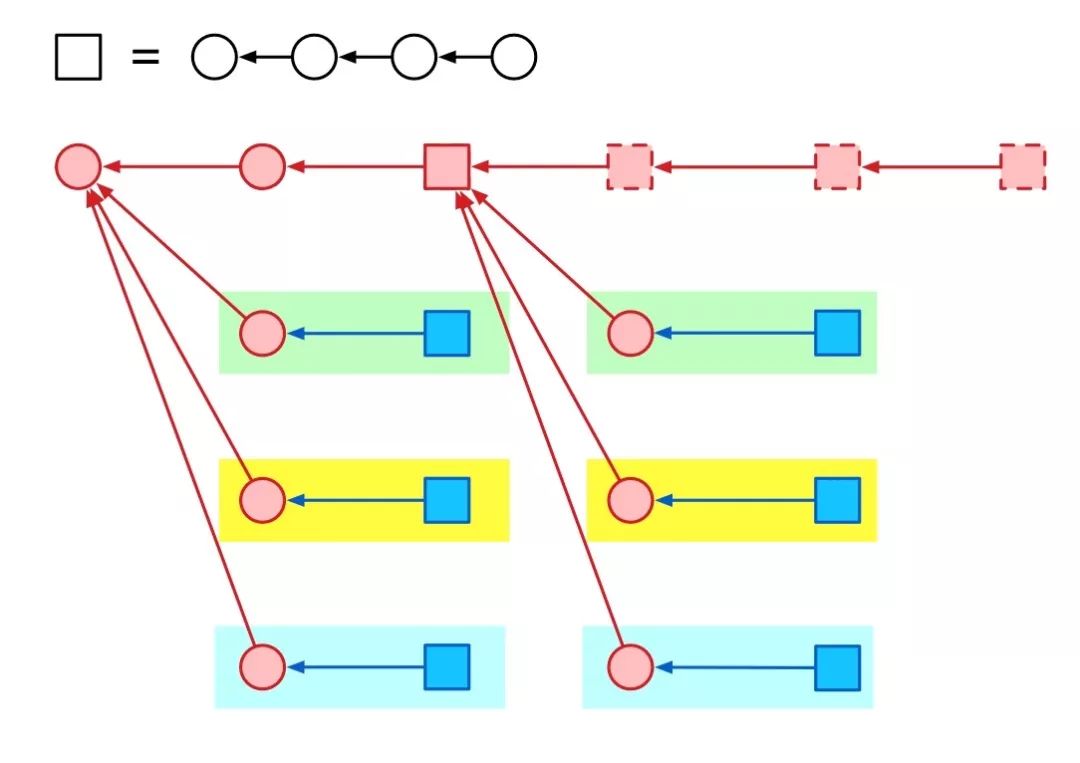
In each round, if a good person generates an average of 30 blocks, there are an average of 10 blocks under each subtree.

The attacker only needs to broadcast 11 blocks (possibly because the randomness is slightly more) to complete his purpose. At the same time, the attacker can generate 20 new blocks.

The chain that the attacker hides will be longer and longer. Moreover, every block in this chain will eventually become the main chain recognized by all honest nodes. In other words, the attacker controlled the main chain with a block that has been hidden for a long time.

If a block was hidden by an attacker for a long time, it later became the main chain recognized by all honest nodes. This is a terrible thing. The attacker may have hidden enough blocks in the subtree of this block. It can broadcast these hidden blocks at any time, forming a large weight. The subtree is used to defeat the subtree of the good man.

Thus, if there are transactions in the good Son Tree that have been confirmed, then the confirmed transactions will be reversed. In other words, the attacker completed the "double flower attack."

Fortunately, a block has been hidden for a long time, although it is difficult to judge under the most heavy chain rules, but combined with the "tree structure", we have the ability to find those main chain blocks that have been hidden for a long time.

If we postpone the confirmation of the transaction after this block, we can avoid being double-flowered.

However, this brings another problem, that is, the transaction is delayed and cannot be confirmed. In general, under the reasonable confirmation rules, "segmentation attacks" can only achieve "survival attacks."

So, using the tree diagram structure, are we capable of detecting this attack? After detecting this kind of attack, what is the response?

We will continue to update Blocking; if you have any questions or suggestions, please contact us!