AMM Triangle Liquidity Providers, Options, and AMM Translation

AMM Liquidity Providers, Options, and Translation

Compiled by: Antalpha Labs

Today, we had a very interesting discussion with Guillaume Lambert from LianGuainoptic and Mark Richardson from Bancor/Carbon, involving liquidity provision (LP), trading, and automated market makers (AMM). I would like to briefly present some thoughts that I have been pondering for a while, which are interconnected but I am not very sure how they apply.

Note: Guillaume Lambert is a professor who is very active on Twitter, Medium, and the Uniswap community. He has his own project called LianGuainoptic and has also engaged in many discussions on LP and options.

The key concept I want to describe is something I would like to call the “AMM Triangle“. On the one hand, it represents the relationship between different participants in an AMM (liquidity providers and arbitrageurs), and on the other hand, it involves options traders (especially hedging option buyers). Let’s start with this triangle:

• REPUBLIK completes $6 million in seed funding, with a valuation of $75 million.
• LianGuai Morning News | Brazilian official suggests prosecuting Binance executive SBF, whose ambition is to become the President of the United States.
• Inventory of 16 Israeli concept coins worth paying attention to, with infrastructure and DeFi as the main force.

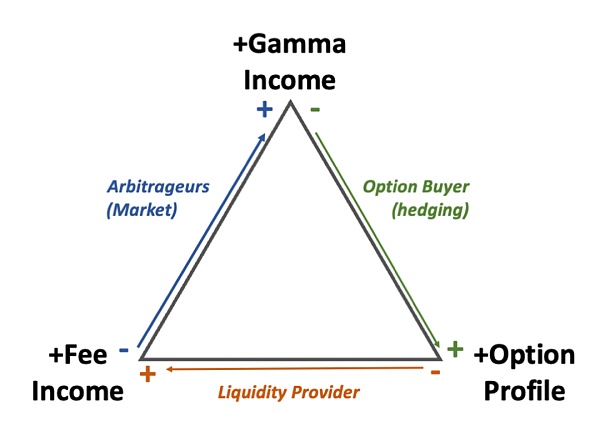
AMM Triangle

This concept represents three value flows (for lack of a better term) related to an AMM position:

1. The fees received by liquidity providers every time they trade on an AMM

2. The option combination corresponding to impermanent loss, considering a portfolio that holds a call option (matched with the square root allocation described in [1])

3. The Gamma income corresponding to option hedging and AMM position rebalancing

Note: The square root allocation refers to the relationship between the value of an ETH-USD Uniswap position and the ETH-USD price, which is a square root relationship. This will be explained in more detail in a separate article. Call options are also referred to as general options.

Now we have identified three typical market participants, each occupying one side of the triangle, which means they are short at the corresponding vertex and long elsewhere. Specifically:

1. Liquidity providers receive fee income but are short in terms of the option combination, which includes impermanent loss [2] and the corresponding square root option returns [3]

2. Arbitrageurs are short in terms of the income from trading fees, but they can obtain Gamma income corresponding to impermanent loss

3. Options traders hold option portfolios for the long term and hedge them, thus holding short positions on Gamma income

I discuss these topics in more detail in the AMMs and Financial Derivatives chapter of theammbook.org [4] paper. Here, I will only provide a high-level intuition.

The situation of liquidity providers: The AMM design gives them fees, and the research on the square root options corresponding to the impermanent loss of AMMs with a constant product k=x*y has been almost completed. Similarly, the option characteristics of concentrated liquidity correspond to option combinations within the liquidity range.

Arbitrageurs are bears on transaction fees – this is the cost you pay when trading on an AMM. What may not be immediately apparent is that they are also bulls on gamma. To understand this, the key piece of information is that an arbitrageur’s trades move the price from P0 to P1, with the average execution price being the geometric mean sqrt(P0*P1). What does this mean? Let’s use the standard assumption of no end customers, deep market depth, and good liquidity, with arbitrageurs trading between the market and the AMM. In this case, it is well known that AMMs will be continuously arbitraged so that their marginal prices correspond to market prices. So what happens when the price moves from P0 to P1 and back? As we have seen before, the AMM buys and sells at the same price, i.e., the geometric mean. However, the arbitrageur has bought at the price of P0 and sold at the price of P1, capturing the full market move – this is their “gamma income,” and it can be easily shown that this gamma does indeed correspond to the “temporary loss” revenue profile of AMMs.

For options traders, it is similarly well known: if a trader holds an options profile and delta hedges it, then – only in the ideal Black Scholes world, of course – their delta hedging cost exactly matches their payoff at expiration.

This model has some basic flaws to consider, partly because arbitrageurs and traders are being discussed in very idealized market environments, which raises some fundamental questions, such as:

• If there is a market with both deep and liquid depth, why do we need AMMs? Why don’t people trade on that deep and liquid market?

• The world is not a Black Scholes world, and delta hedging is not a perfect replication strategy.

• Arbitrageurs have the right to choose not to trade, so they will only participate when their gamma income exceeds the fees they pay; gamma is equivalent to options payoff at expiration, so fees can never compensate for temporary losses.

The reality is that market microstructure is much richer than what is implied by Black Scholes and deep-liquid market assumptions. In the real world, everyone has their position. However, in my view, the AMM triangle provides a good structural indication of how these different aspects are interconnected and how they can be combined to extract certain specific liquidity, especially liquidity related to options.

We will continue to update Blocking; if you have any questions or suggestions, please contact us!