Zero-knowledge proof study notes: background and origin

Subtitle or Abstract: Zero-Knowledge Proof Study Notes for Stanford Academy (1)

The author of this article, Dong Ze, a small partner from the Abe technology community, is currently studying at Stanford University and researching cryptography. This series of articles is derived from the author's study notes on Stanford's famous course "CS 251: Cryptocurrencies and blockchain technologies. The course teacher is Dan Boneh of Cryptography.

I learned about blockchain and digital currency related technologies with Dan Boneh in Stanford last semester. Unlike previous courses, this year's course has a new chapter called Zero Knowledge Proof. Mengmeng Dan and his great god phd Ben Fisch took turns taking lessons for us, and spent two weeks teaching the origins, concepts and realization of zkSNARK of zero knowledge.

After completing the final exams in these two days, I reviewed the whole class in my mind repeatedly during the review process. I felt that the most exciting part was the zero-knowledge proof. I think about taking advantage of the recent holidays to summarize and share with you.

Foreword

After writing the first draft, when I shared it with my friend Proofread, I found that many friends reported that their background knowledge was not enough. So I added this chapter before I started, marking out the background reading needed to understand this article:

• Can Ethereum survive without monetary policy?
• "Blockchain + insurance" is not without disadvantages, two major problems to be solved
• Free and easy week review 丨 US government agencies research fiat cryptocurrencies through fork BTC

1. Merkle Tree / Merkle Proof : https://blog.csdn.net/wo541075754/article/details/54632929
2. Bitcoin transactions : https://blog.csdn.net/liduanwh/article/details/81141972
3. UTXO model : https://www.jianshu.com/p/02fd289e8853
4. Some basic encryption and decryption concepts : https://www.jianshu.com/p/f7c729a41c9f

After reading the preface, we can start the text .

To say that zero-knowledge proof is really hot in everyone's field of vision, in fact, we have to start with Bitcoin.

Deficiency of Bitcoin

If you are familiar with Bitcoin, everyone should know that on the Bitcoin network, every transaction is public.

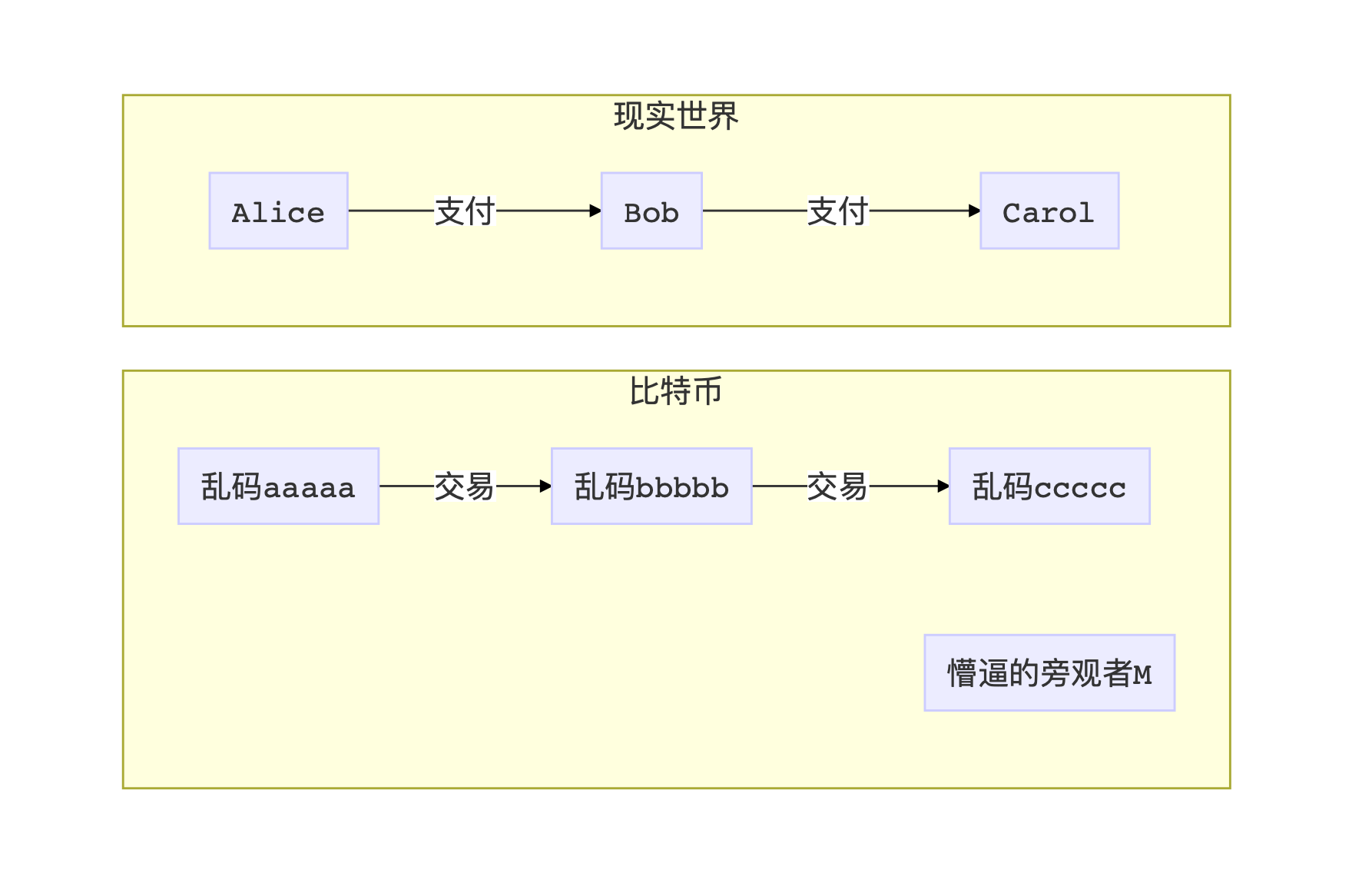
If A wants to pay B a sum of money, then A will announce to the entire network with a big speaker, she will create a new transaction (Tx), and the beneficiary of this transaction is B's public key (P2PK), Or the hash of the public key (P2PKH). As long as B sees the transaction, he can use his private key to sign a digital signature to prove that he is really the owner of the public key, thus spending the money.

When A submits the transaction to pay B, as a bystander M on the network, she can only see a bunch of garbled addresses aaaaa pay x coins to a bunch of garbled addresses bbbbb. When B then made money to C, he could only see that bbbbb made a sum of money to ccccc. We can see that transactions in Bitcoin are highly connected. Although we don't know who paid for it, we can find many transaction chains along the way.

If every user just makes good money back and forth, Bitcoin is actually relatively safe.

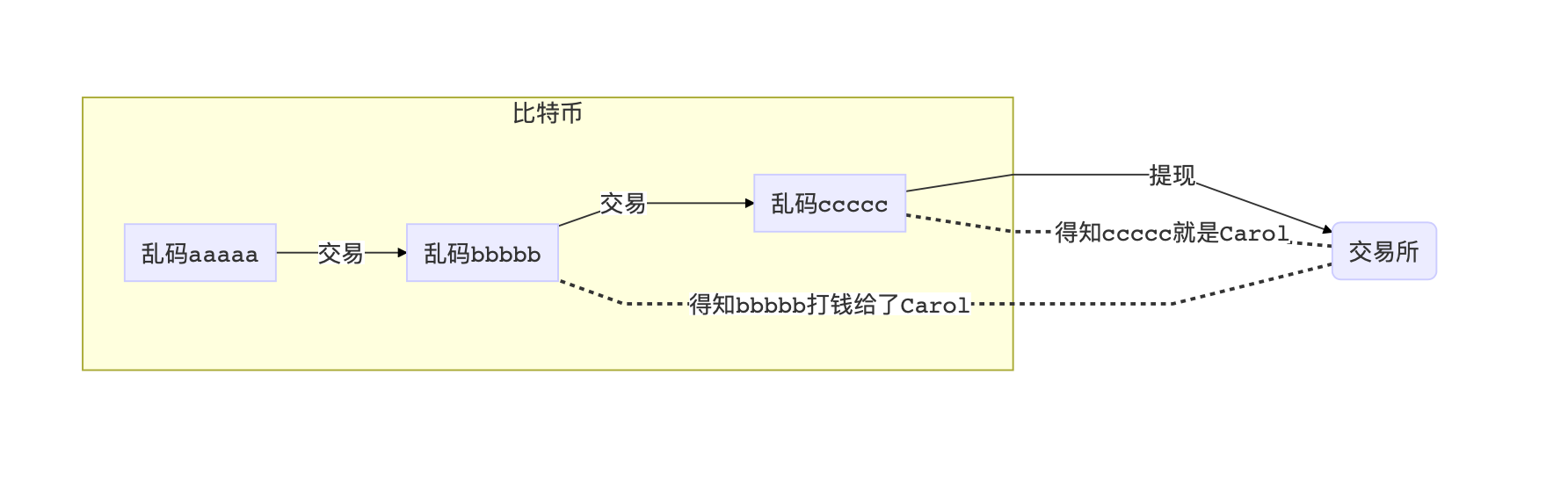
Once a user sees it, does not want to play, and wants to go to the exchange to cash out, then the transaction information of this entire chain will be exposed. Exchanges often have a KYC (Know Your Customer) policy, and each user who exchanges digital currencies and fiat currencies needs to undergo real-name authentication. Once C withdrew from the address ccccc and ran away, then the exchange grasped the fact that bbbbb once sent money to C. If C is suspected of money laundering, just need to wait for B to cash out at this time, and then grab it.

There are already many companies in the United States doing analysis on the transaction chain of Bitcoin, such as Chainalysis.

Presumably here, everyone can feel the deficiencies of Bitcoin: the randomly generated public key for receiving money is just an illusion (net name). Once the real-name system is authenticated, the net name and the real name are linked, then online before All that is done is unobtrusive and there is no privacy at all. This is like someone using a net name to post a message on the post bar, and then someone finds the mobile phone number with a secret security, and then uses the mobile phone number to find the registered real name, so being human is a reason.

Anonymous and Pseudonymous

There are actually two types of understanding of privacy.

The first is Anonymous, which means that users do not have to disclose any information related to themselves. It is like a confession wall of a school. You can never know who wrote it. Anyway, it is written on it.

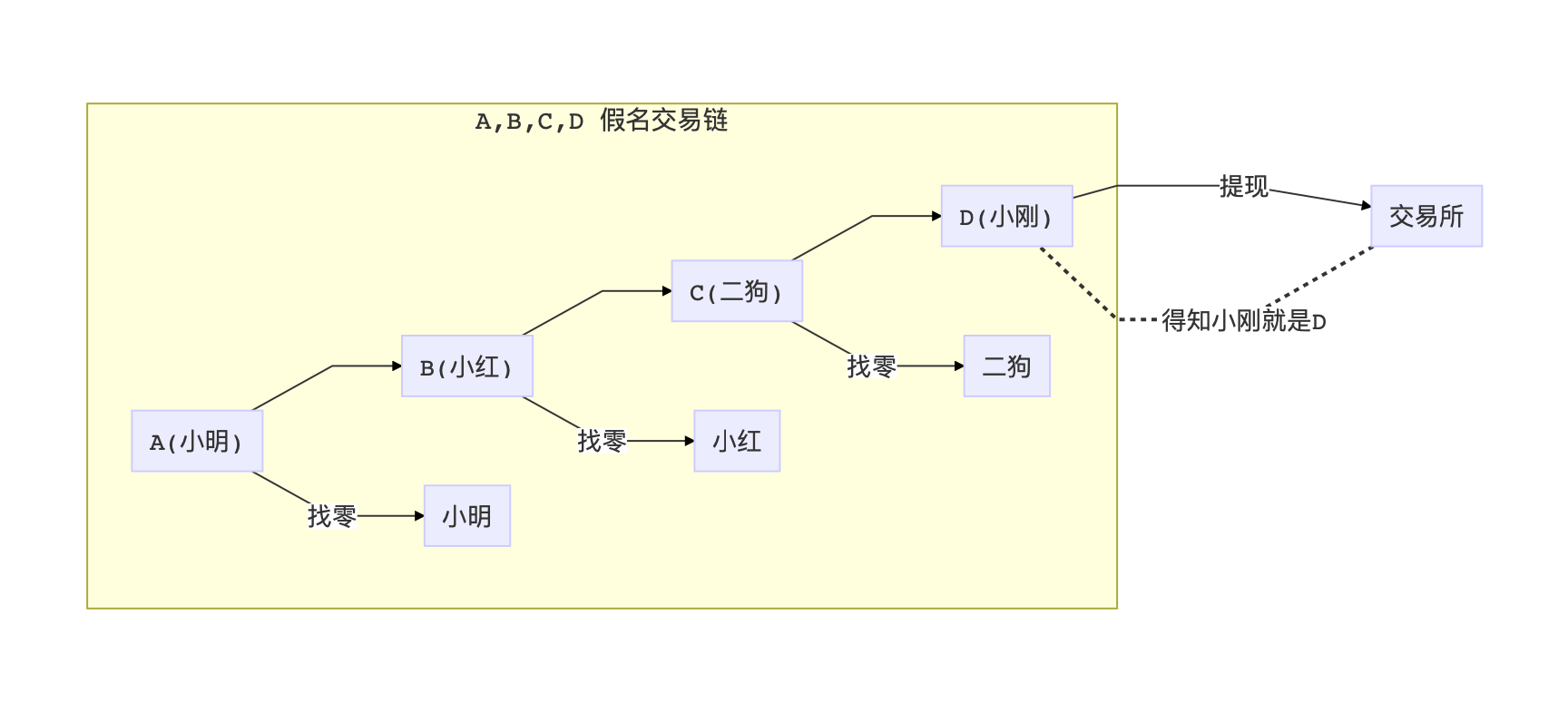
The second is Pseudonymous, which means that users post information using their own pseudonyms. It is like posting. If you do n’t know this user, you ca n’t establish a connection from the real name to the real name, and you do n’t know who posted it. who is it.

Looking at this analysis, Bitcoin is actually a pseudonym mechanism: each user will randomly generate his own public key (alias), and receive money through the public key address. This is like four people A / B / C / D aliased as Xiaoming / Xiaohong / Two Dogs / Xiaogang anonymously trade online, as long as D reveals his identity at any point (such as on the exchange Withdrawal), then the relationship between Xiao Ming / Xiao Hong / Egou and D will be exposed immediately.

We can discuss how to enhance the confidentiality of Bitcoin from these two methods.

Ways to increase privacy

CoinJoin

Since A pays B to be seen, and C pays D to be seen, some people think of simply throwing all four ABCDs into one transaction. Because bitcoin transactions can have multiple inputs and outputs, an onlooker will see that in a transaction, aaaaa and ccccc both put x coins into it, and then bbbbb and ddddd receive money. In this way, even if the transaction income knows that these addresses correspond to the four ABCDs, it is difficult to distinguish who received the money.

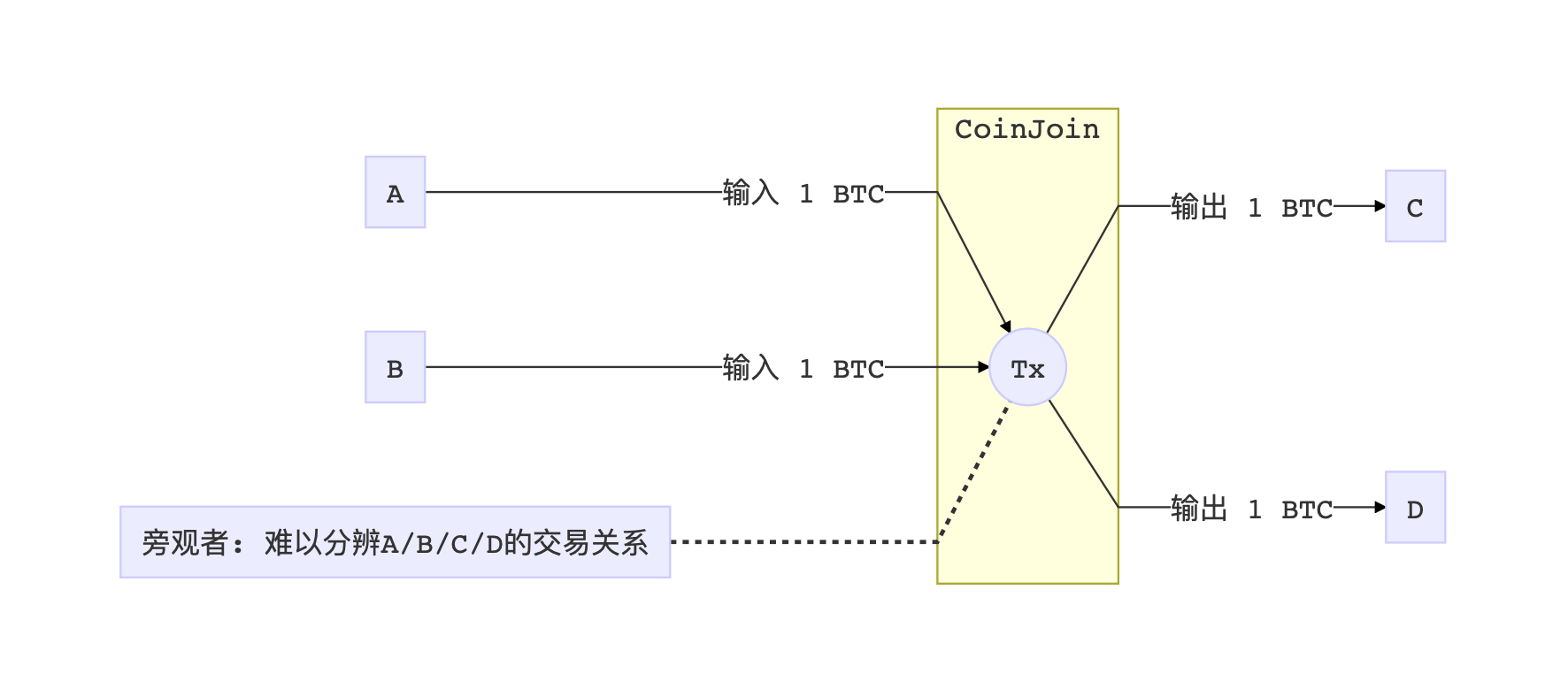
What if the two sets of transactions are still too easy to identify? Two is not enough to mix four, four is not enough to mix eight, and so on. Combining the transactions of various people together, confusing audiovisual, making it impossible to track. This is CoinJoin.

What are the disadvantages of CoinJoin? In fact, mixing multiple transactions does not completely prevent people from being touched. It can only be said that the probability of being touched all the way is reduced in probability. And there is another important point, if you want to mix AB and CD transactions, then their transaction volume must be the same. If A pays 10,000 coins to B and C pays D coins, we only need to look at the input and output to immediately split a CoinJoin transaction into two separate transactions. Therefore, mashing up transactions with similar transaction quotas is also a difficult point for CoinJoin to implement.

If you look at the above classification, CoinJoin is just an operation of Bitcoin's existing system, and its essence is still a pseudonym mechanism.

Confidential Transaction (CT)

Since it is so troublesome to hide who I am, then people start thinking: if we don't hide the public key that participates in the transaction, we can also hide the transaction amount. When A pays B, even if B is exposed, the entire network will not know how much A has given B.

If this step can be realized, then we can even pay with bitcoin. Everyone can only see that your monthly salary is received, but we don't know how much money you make.

To implement the method, we must first understand a special encryption algorithm: homomorphic encryption.

In a word, homomorphic encryption is a special encryption algorithm that allows the ciphertext to retain its original mathematical characteristics .

We can assume that there is an encryption method E. If E is an addition homomorphism, then E (a) + E (b) = E (a + b). Conversely, if the multiplication is homomorphic, then E (a) x E (b) = E (axb).

Since this article is about the popular science of zkp, we don't know the specific implementation method in detail. We just need to understand that both the ellipse encryption equation and the large number module in RSA have some kind of homomorphism.

Pederson Commitment

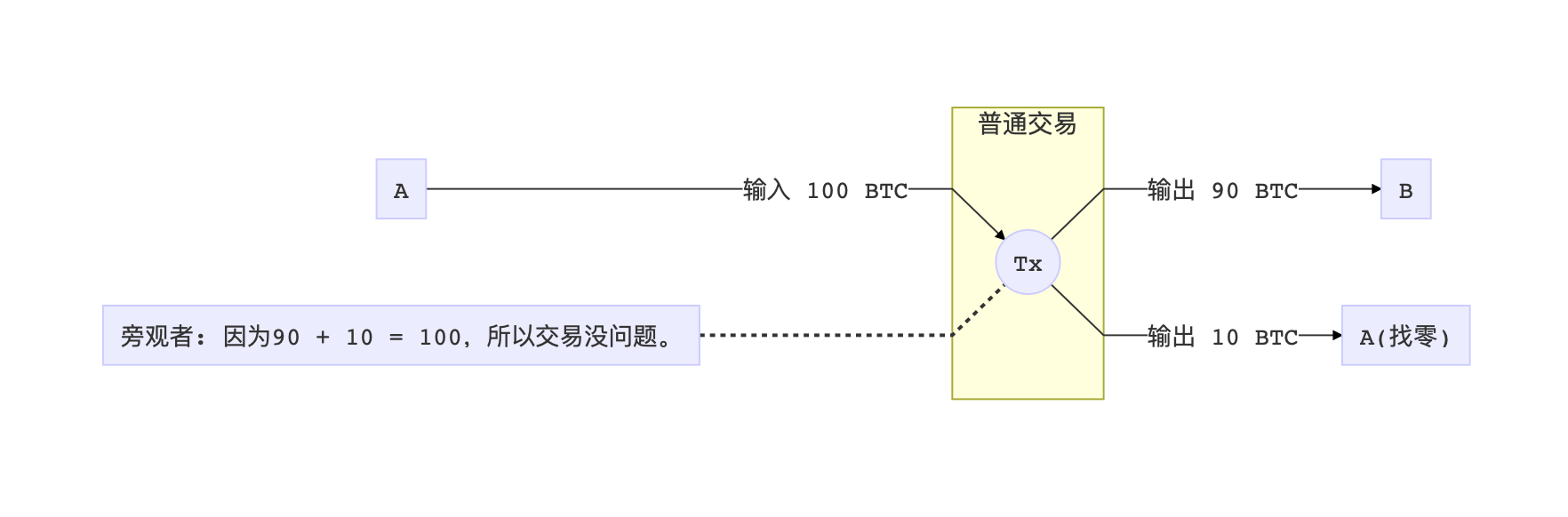
Continue to the topic of hidden trading volume. If A has a balance of 100 coins and pays 10 coins to B, then this transaction would look like this:

Combined with the addition homomorphism mentioned above, if we have an encryption homogeneous method E, we can convert this transaction into:

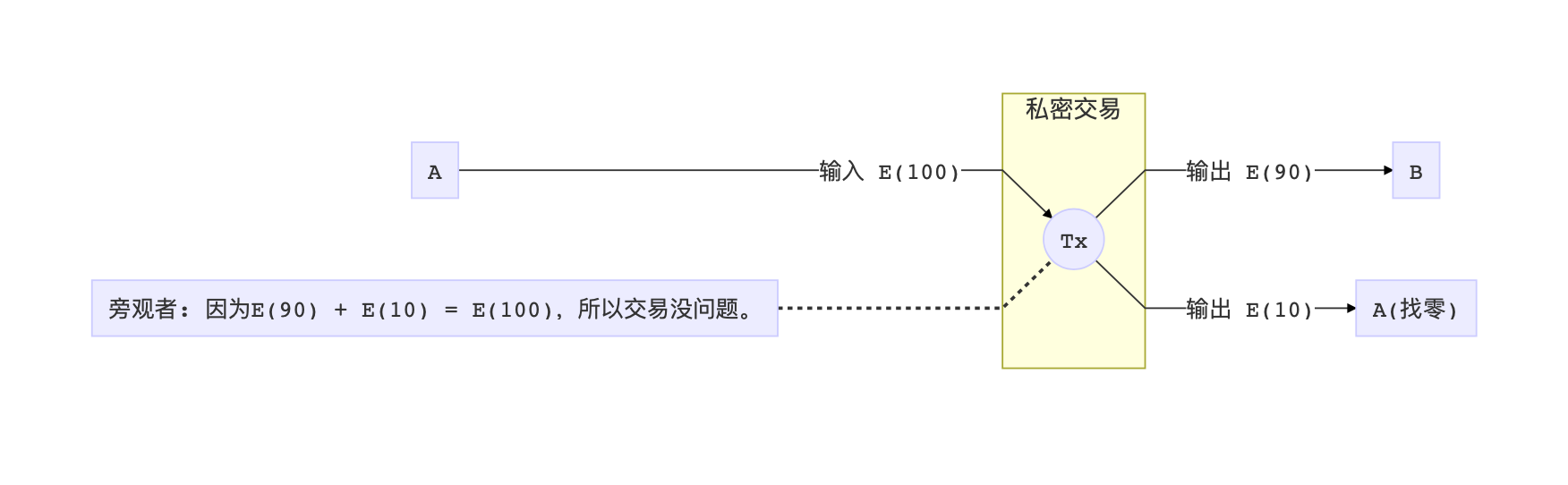
As long as the first number is equal to the sum of the last two numbers, an onlooker will not see the transaction volume in the end, but has to admit that A really divided some money to B, and then some money was returned to A . This method is called Pederson Commitment, which hides the data itself, but proves the relationship of the data.

Negative number loophole

After reading this, some friends will find a huge loophole: Although Pederson promises to prove the relationship between numbers, it does not limit the value range of any number! That is to say, A can do bad things, submit a transaction, say that he has to pay -100 coins to B, and then "find" himself 200 coins, so that the equation still holds true. A can use this to print unlimited banknotes, thereby destroying the entire system.

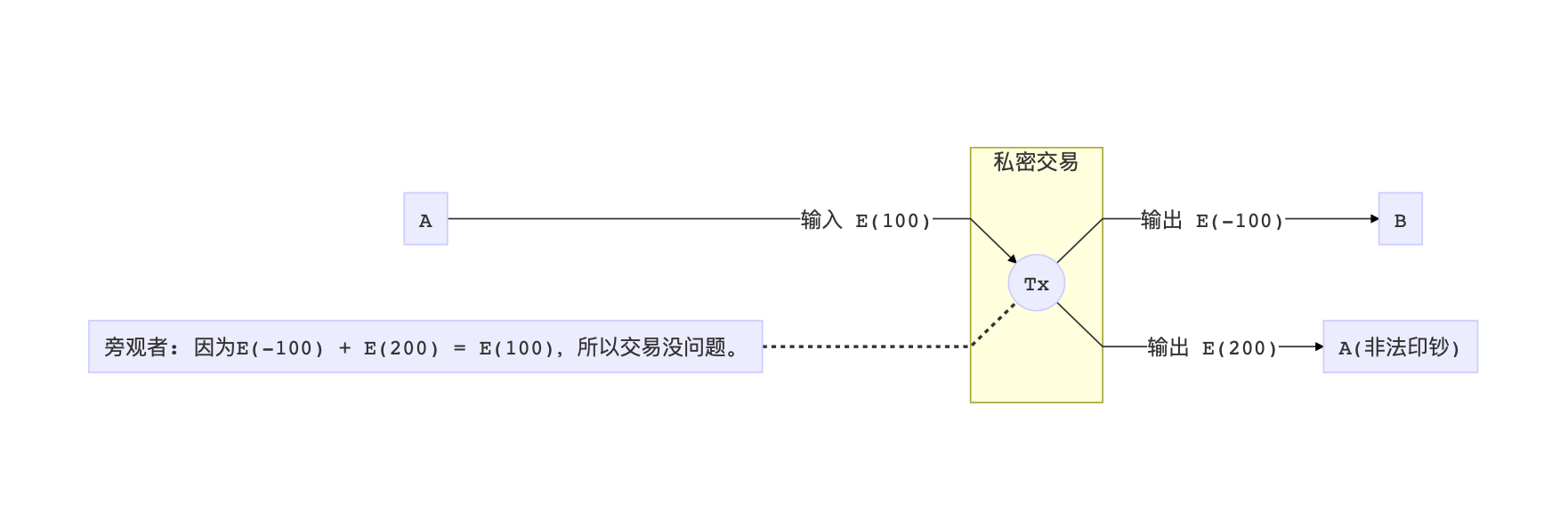
How to avoid negative numbers? In addition to Pederson's promise, we need another set of proofs to prove that the numbers in all transactions are positive. In other words, the numbers in all transactions are limited to the range 0 to 2 ^ 256 (positive integer maximum) (Range Proof).

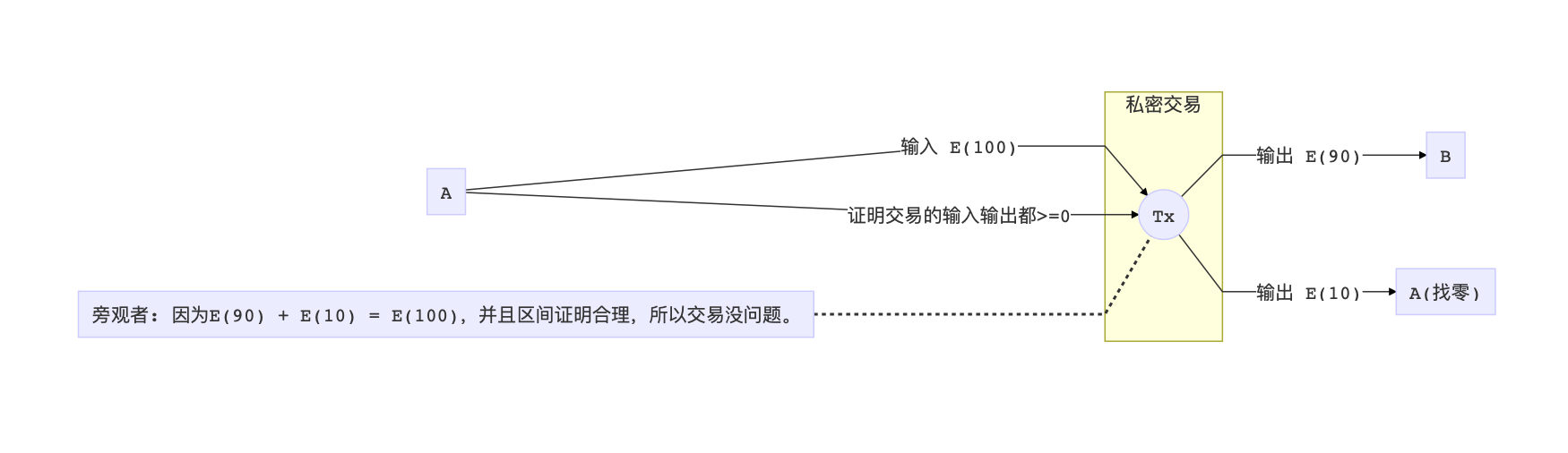
It doesn't sound difficult, the easiest way is undoubtedly to make all these figures public. But this violates the premise of hidden trading volume. So we have to find another way to prove it, that is, we can't expose the original numbers, but also prove their characteristics (values ​​are 0 ~ 2 ^ 256). Does that sound like a problem? Don't worry, let's look at another problem.

Ownership loophole

Before we go any further, I want to quickly point out that there is still a huge loophole in this agreement: ownership is unknown.

Friends who know bitcoin may know that when creating a bitcoin transaction, you need to provide the UTXO Txid of the input transaction, so that you can quickly verify whether the A who is preparing to pay B really has the money .

But right now, we haven't mentioned anything about pointing to the previous transaction. In other words, because the entire network does not know how much A has spent, A can simply change the input number to whimsical, and change it to tens of thousands, and then call them all to secretly mint coins.

how to solve this problem? There are two options.

The first solution is to continue to introduce Bitcoin's transaction mechanism, and use the output of the previous private transaction as the input of the transaction. This kind of thinking is a bit like the conversion of a problem. I use the result of the transaction for this transaction, so long as the transaction is OK, my transaction is not problematic.

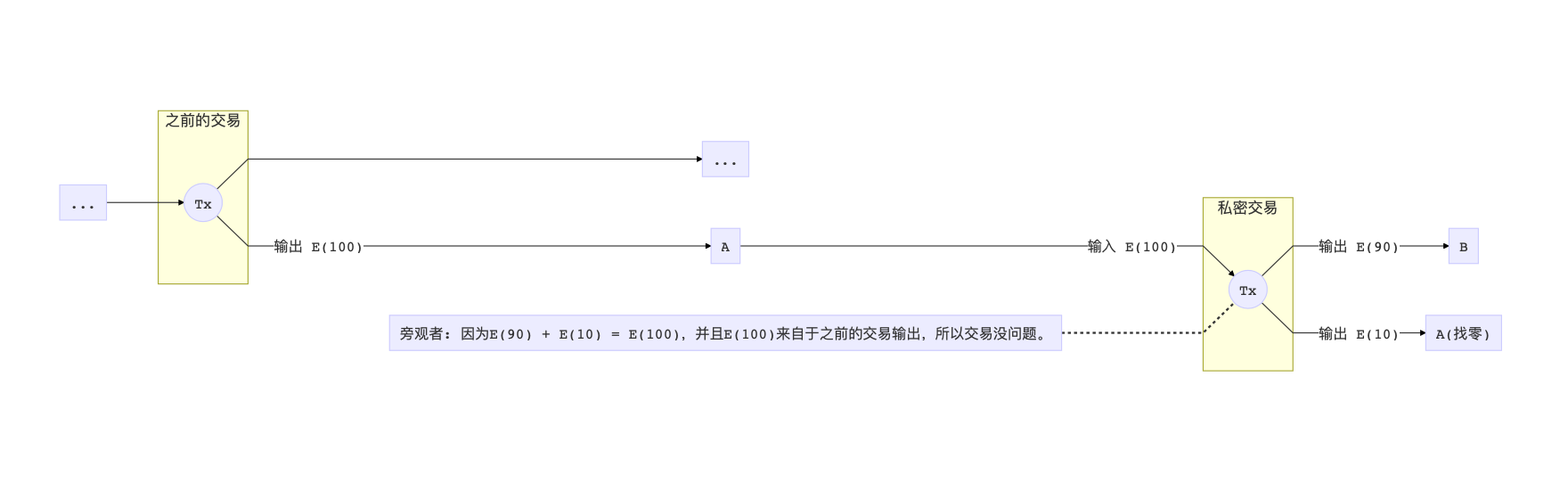
This is a chicken and egg problem. How to create the first private transaction without problems?

We can convert ordinary coins into private output through a special transaction. The input of this transaction is an existing transaction id (Bitcoin UTXO), and then the output becomes a privacy output. So we have the earliest eggs. (ZCash's shielded transaction is this principle)

The second solution is to prove that the input of A really belongs to A. In systems like Ethereum, there is a concept of a World State. The world state is the current balance and state of all users and smart contracts on the entire chain. Generally, a complete node will retain the entire world state (large size), while a light node only needs to save the world state Merkle Commit.

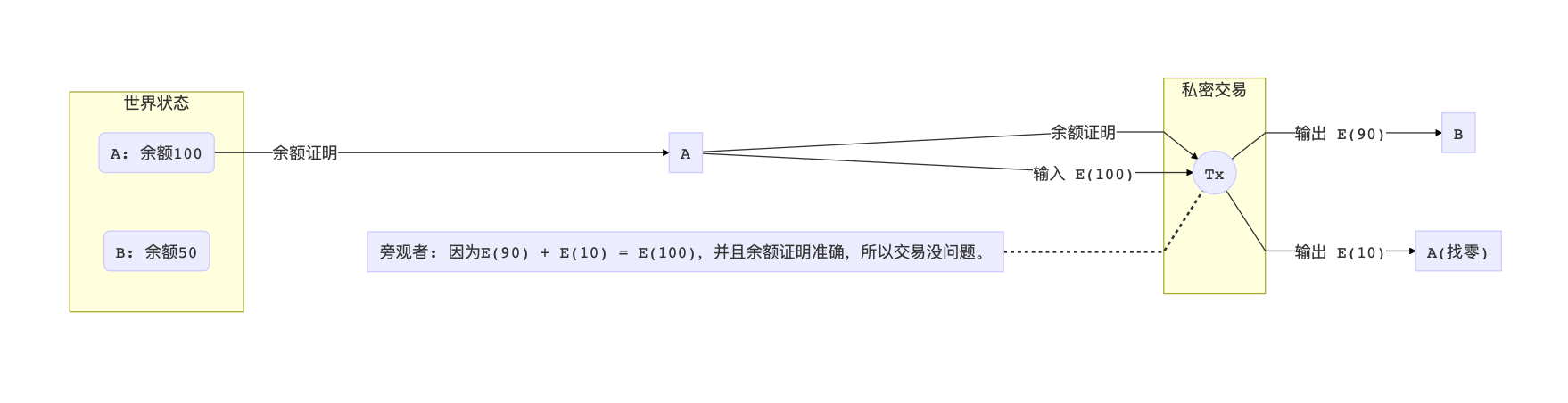
In addition to the Pederson commitment and interval proof, we provide an additional proof that the number entered in the transaction is consistent with the balance of A in the original world state. We can use Merkle Proof to achieve this proof.

But if we directly submit Merkle Proof, all bystanders can see the transaction input of A, which violates the premise of private transactions. So again : we still need to borrow the mysterious algorithm mentioned above-it can hide the answer itself (the balance of A), but it can also prove that this number really belongs to the world state.

ZCash: All anonymous

When the concept of CT was put forward, many people were dissatisfied with the status quo and couldn't help feeling: If only their names could be hidden.

Therefore, the concept of ZeroCoin / ZeroCash was proposed: based on CT, but with the addition of a new mechanism, the users of the transaction can be anonymous. At this time, onlooker C, who was eating melon, was really aggressive, and saw a bunch of garbled characters floating on the network, but he didn't know what it was, but he had to believe it.

ZCash is a digital currency based on the ZeroCoin / ZeroCash protocol, which can achieve full anonymous transactions. I won't describe too much here, but it still relies on the old cryptographic tools: Pederson promise, interval proof, Merkle proof, and the black magic we have been mentioning: it will not expose the answer itself prove.

After all the calls came out, we finally have to talk about the highlight: this proof method that does not expose the answer itself is called zero-knowledge proof.

Zero-knowledge proof (zkSNARK)

I believe that after reading the above, everyone has probably understood the problem we want to solve.

We want to prove the relationship between numbers, such as 0 <= a <= 2 ^ 256, or SHA256 (x) = y. But we don't want to expose these numbers, such as a and x in the previous article. How to build a system to achieve this?

Before talking about this topic, I want to change my mind and split this topic into two parts: zero-knowledge (zk) and proof (SNARK) .

As always, let's talk about definition and application first, and then how to implement it.

Proof (SNARK)

Let's start with proof.

The full name of SNARK is Succinct Non-interactive ARgument of Knowledge. This noun consists of three dimensions:

1. Succinct: The proof itself must be short enough. It is best to verify that the proof is O (logN) or even O (1) complexity.
2. Non-interactive: There is no interaction in the overall process, which means that the proving party can throw a bunch of garbled characters on your desk and then leave, and you can verify the garbled characters after you verify it. prove.
3. Argument of Knowledge: This stuff is more obscure. But the general meaning is that what you want to prove must be capable of expressing knowledge (Proof of Knowledge). The proof of PoK involves a more abstract concept of Extractor. For details, please refer to Teacher Yu's article. But in a word, the thing you prove is valuable, calculated through calculation, not messy other things.

After looking at the definition, we will find that it is already very strong to realize SNARK, especially in the short point.

We can immediately think of an application: if a third party organization stores a large amount (PB level) of data in its own database. If a government agency wants to audit their database to ensure that there is no problem with each data point, it may be necessary to look at it line by line, look at each PB's data, and see that the land is old. At this time, SNARK suddenly appeared, and the size and time of O (1) or O (logN) fully proved that there is no problem with each data in this huge database, and I was a little excited about it. Most people think this is completely impossible: how can you verify the accuracy of tens of millions of digits with a few digits?

Leave a suspense and talk about it later.

Zero knowledge (zk)

We return to zero knowledge.

In fact, zero-knowledge is just an additional requirement on the basis of this SNARK proof: the entire proof itself cannot expose any data about the mystery to be proved. The official definition of the concept of zero-knowledge is very obscure and introduces the concept of a simulator. For a detailed introduction, you can still refer to Mr. Guo Yu's article, I will take it here. In a sentence, a clever hacker can't extract any information related to the answer by holding a zero-knowledge proof.

Returning to the concept of the government audit database, we can assume that this database is the tax situation of the company. The government must make sure that the tax payment data must be accurate, but for companies, they don't want the inspectors to see their daily business flow, because it may involve trade secrets. At this time, one SNARK is not enough. We need zkSNARK to achieve:

It can prove that I paid the tax truthfully without showing you the details of each of my transactions.

Application of Zero Knowledge Proof

What can we do with zkSNARK?

The first thing is to implement the Private Transaction mentioned above. ZCash's private transaction mechanism is based on zkSNARK. In this way, digital currency transactions become much safer.

Second thing, we can use this technology to better solve the problem of blockchain efficiency . At present, there are undoubtedly several methods for blockchain scaling: sacrificing the strength of consensus to increase the block speed, enabling sidechains, or offline point-to-point channels similar to Lightning.

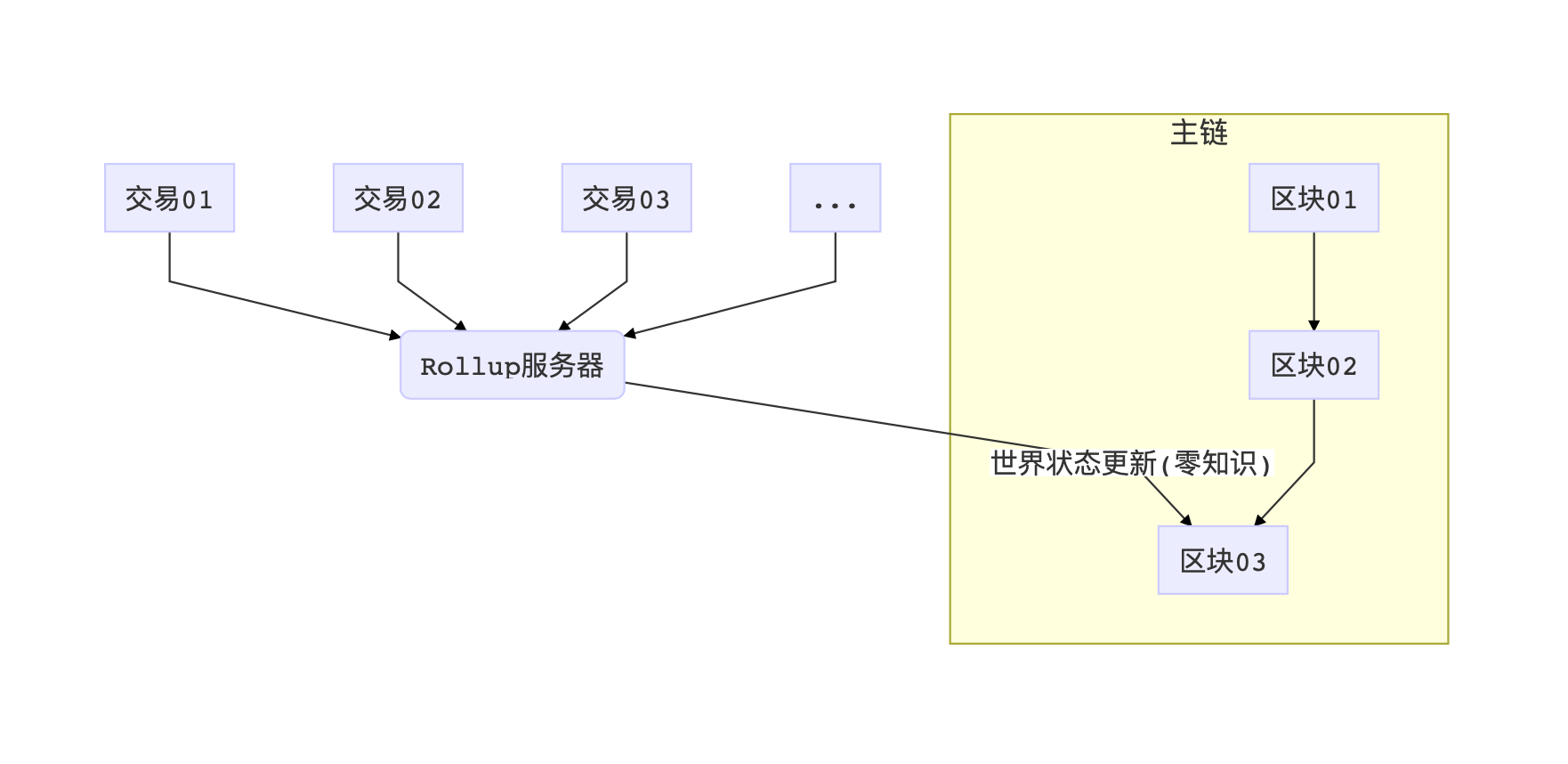
In fact, there is another idea called Rollup. The concept of Rollup is probably that the load on the main chain is too large, so we open a few small servers, can also receive transactions, do transaction authentication, and then batchly accumulate all the transactions accumulated over a period of time. Update to the main chain. But if this update process still needs to send a large amount of transaction information to the main chain, the significance of this Rollup will not exist, and it will not reduce the load of any main chain. At this time, SNARK comes in handy: With SNARK (zk or not), the Rollup server can submit to the main chain with a very short certificate, which proves that a large number of transactions are OK. As a result, adding some UTXO and reducing it is done. With ZK Rollup, we can greatly reduce the load on the main chain and outsource more verifications elsewhere.

The third thing is that we can really implement transactions to third parties .

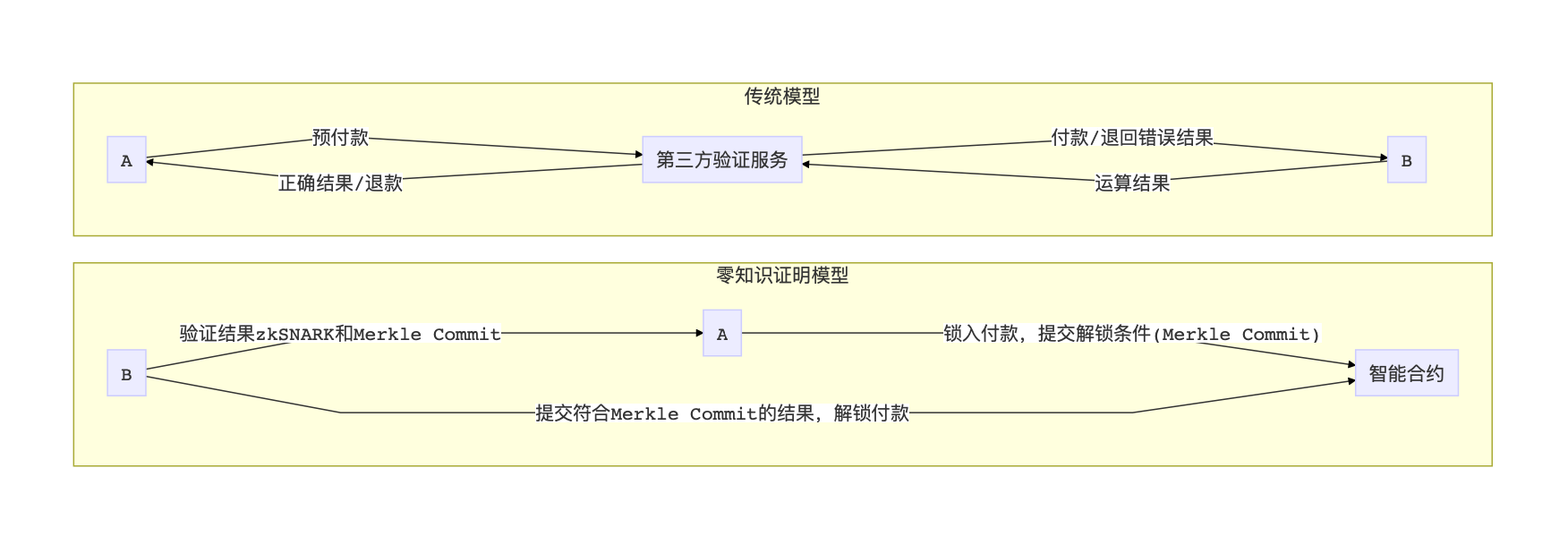
Suppose A is doing machine learning research, but does not have a good computer, so she plans to outsource the task of training the model to B. After three days, B told A that he was finished running, and he needed to ask A to pay before providing her with the trained model. A is worried that B does not train the model honestly, but randomly generates a random number and packs it, so he wants B to first pass the model to A and then pay. B was worried that A secretly copied the model after getting it, and then pulled him directly without giving money.

Faced with this type of problem, the traditional solution is to entrust a third party or design a smart contract on the chain to complete the verification and exchange of data and currency. Now with zkSNARK, B can directly submit a model-trained zkSNARK to A, proving that he really ran for three days without cheating. After passing the quick verification, you can safely pass the money.

The fourth thing, we can completely transfer the ownership of the data .

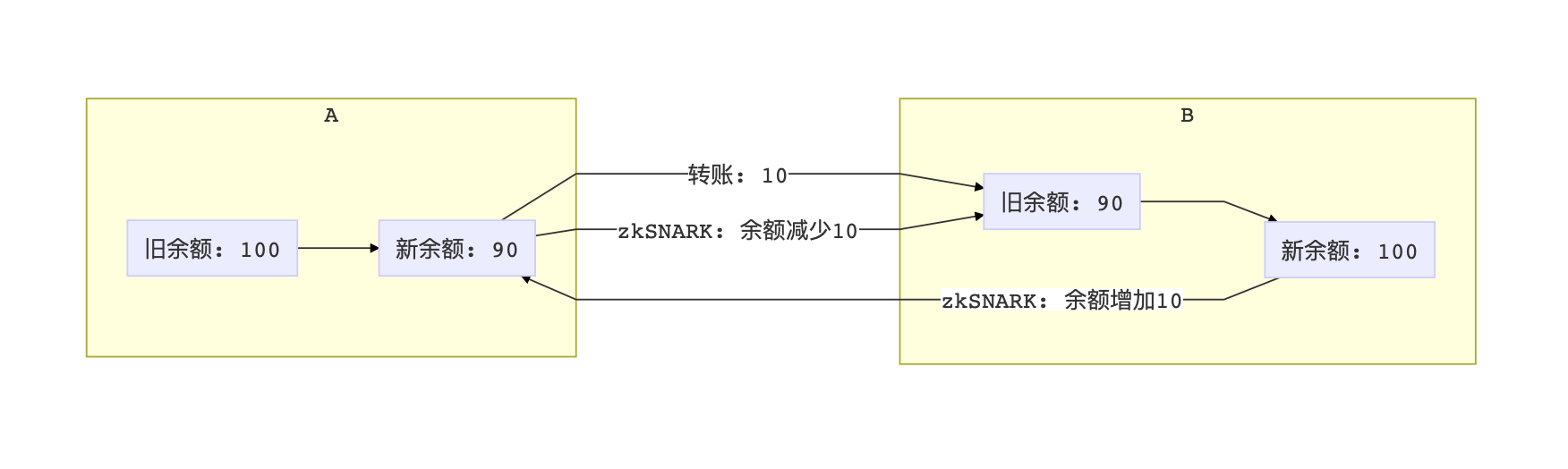
Assuming the bank's account balance database is a sql table, then 100 million customers will have 100 million rows of records. Every year banks need to spend a lot of money to maintain such a large data system. If everyone can move their own line of records to the local area and maintain their own account data, then the bank will not have to spend a penny. The reason why the bank does not do this is because users are likely to tamper with their own data for the benefit of turning 100 yuan into 1 million.

zkSNARK can guarantee that the data itself will not be a problem. We can imagine a distributed bank where everyone's deposit balance is stored in their own computers. When A wants to transfer money to B, she needs to submit a zkSNARK that proves that the balance on her account is deducted correctly, so as to ensure that A honestly deducts the transfer amount from her balance. When B enters the account, it will also submit a zkSNARK with an increased balance.

We can apply this concept to all areas, social networking, banking, health, financial auditing, corporate taxation, etc. With zkSNARK, service providers do not need to pay for the storage of large amounts of data, and users do not need to worry about their privacy being stolen.

To be continued

For reasons of space, this is written here. I must see here, everyone has a deeper understanding of why zero-knowledge proofs are needed and how powerful they are.

Beginning in the next article, I will write a little more in-depth, and mainly discuss the specific structure of zkSNARK.

PS: Zero-knowledge proof and zkSNARK are used interchangeably in this article. In fact, zkSNARK is just one of the more classic zero-knowledge proof protocols, and there are many other protocols that will be introduced later.

Read more

If you want to know more about what is in this article, I have collected a Reading List and put it below. Interested friends can read.

1. Teacher Guo Yu's zero-knowledge proof (four articles in total) : https://www.jianshu.com/p/38ab873ae8ce
2. Stanford courseware and after-school reading : http://cs251.stanford.edu/syllabus.html
3. Construction of ZCash : https://www.jianshu.com/p/4db439c63a96
4. CoinJoin : https://en.bitcoin.it/wiki/CoinJoin
5. Confidential Transaction : https://www.jianshu.com/p/22664259dee3

We will continue to update Blocking; if you have any questions or suggestions, please contact us!