Construction and Case Studies of zk-SNARK

Constructing and Studying Cases of zk-SNARKs.

TL;DR

• What is the construction process of SNARK?

  The problem to be proved – arithmetic circuit – R1CS – polynomial

• Why convert to polynomial in the end?

  • Six Catalysts for the Growth of Algorithmic Stablecoin Frax Finance
  • Even Zuckerberg’s Threads is using ActivityPub. What makes this decentralized protocol capable of challenging Web 2.0 giants?
  • Evening Must-Read | Meta Launches Twitter Rival Threads: How to Use and What’s Its Biggest Feature

  Because the characteristics of polynomials effectively shorten the verification time and achieve simplicity.

• How is zero-knowledge achieved?

  Simply put, two random numbers are selected during the derivation of the polynomial, and the polynomial derived from this can make the verifier unable to obtain the coefficients of the original polynomial, that is, the secret input of the prover, thereby achieving ZK.

• How to achieve non-interactive?

  Before the proof starts, a third party, a trusted setup, is introduced, and the task of the verifier to select random numbers is handed over to the trusted setup, thereby achieving non-interaction between the verifier and the prover.

ZK technology has received much attention in the Web3 field in the past two years. Starting with Rollup, more and more projects in different tracks have begun to try to use ZK technology. Among them, SNARK and STARK are the two most commonly heard terms. In order to better understand the application of ZK technology later, this article will simplify the proof logic of SNARK from a non-technical perspective, and then use the zk Rollup of Scroll as an example to illustrate the operation of the zk proof system.

The article aims to explain the basic logic for easy reading, try to avoid using terminology, and will not delve into mathematical conversion and other details. If there are omissions, please forgive me.

In January 2012, Alessandro Chiesa, a professor at the University of California, Berkeley, collaborated with others to write a paper on SNARK, proposing the term zk-SNARK.

zk-SNARK, the full name is Zero-Knowledge-Succinct Non-Interactive Argument of Knowledge, is a proof system that uses ZK technology. It should be noted that SNARK is the name of a class of schemes, and many different combinations of methods can achieve SNARK.

• Zero Knowledge: The content that only the prover knows will be hidden, and no one except the prover can see it.

• Succinct: The generated proof is small and the verification time is fast.

• Non-interactive: There is little or no interaction between the prover and the verifier.

• Argument: The verification of the verifier is only effective for the prover with limited computational power, because the prover with super computational power can forge the proof, that is, the system has computational reliability.

• Knowledge: The prover can only calculate the proof if he knows some information that the verifier does not know.

zk-SNARK aims to solve the “computational verification problem”, which is whether a verifier can efficiently verify a computation result without knowing the privacy of the prover.

Below, we will explain how the system combines zero-knowledge proof to achieve efficient verification by constructing the simplified version of zk-SNARK.

Construction of zk-SNARK

Transform the problem to be proved into a polynomial

In short, the idea of SNARK is to transform the statement to be proven into a polynomial equation.

The whole transformation process: the problem to be proven ➡ arithmetic circuit ➡ R1CS ➡ polynomial ➡ transformation between polynomials

The problem to be proven ➡ arithmetic circuit

To prove whether a problem is true through calculation, the problem to be proven must first be transformed into a calculation problem, and any calculation can be described as an arithmetic circuit.

An arithmetic circuit is usually composed of constants, “addition gates”, and “multiplication gates”. By stacking gates, we can construct complex polynomials.

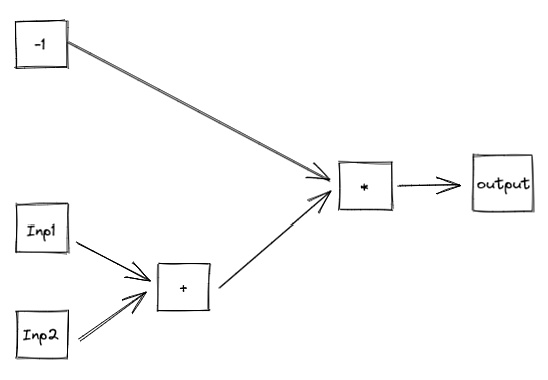
The polynomial constructed by the arithmetic circuit in the above figure is: (Inp1 + Inp2) * (-1) = Output

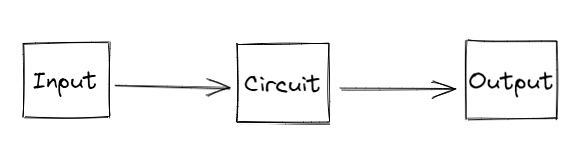
In reality, it is extremely complex to convert problems into arithmetic circuits. We can simply understand it as follows: input some content, the content is converted through the circuit, and finally, output a result. That is:

Based on the concept of arithmetic circuits, we construct an arithmetic circuit for generating proofs, that is:

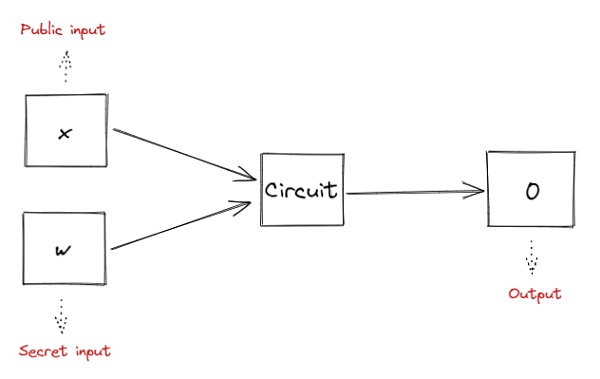
The circuit contains two sets of inputs, public input x and secret input w. Public input x means that the content is a fixed value of the problem to be proven, known to both the verifier and the prover. Secret input w means that the content is only known to the prover.

The arithmetic circuit we constructed is C(x,w) = 0, that is, by inputting x and w into the circuit, the final output result is 0. The prover and the verifier know that the output of the circuit is 0, and in the case of public input x, the prover needs to prove that he knows the secret input w.

Arithmetic circuit ➡ R1CS

We need a polynomial in the end, but the arithmetic circuit cannot be directly converted into a polynomial. We need R1CS as a medium between the two, so we first convert the arithmetic circuit into R1CS.

R1CS, short for Rank-1 Constraints System, is a language used to describe circuits. Essentially, it is a matrix-vector equation. Specifically, R1CS is a sequence composed of three vectors (a,b,c), and the solution to R1CS is a vector s, where s must satisfy the equation:

where “.” represents the inner product operation.

The specific mathematical conversion can be found in Vatalik: Quadratic Arithmetic Programs: from Zero to Hero. All we need to know is that the purpose of R1CS is to describe and constrain each gate in an arithmetic circuit, so that the vectors between each gate satisfy the above relationship.

R1CS➡Polynomial

After obtaining R1CS as a medium, we can convert it into a polynomial. The following is an equivalent conversion between matrices and polynomials:

Polynomial

Converted to a matrix

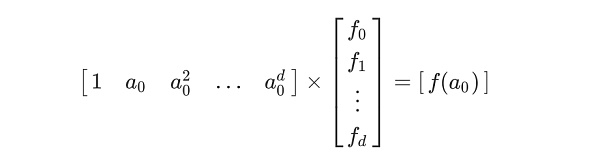
Based on the above equivalent conversion properties, for matrices that satisfy R1CS, we can use Lagrange interpolation to restore the coefficient of each term in the polynomial. Based on this relationship, we can derive the R1CS matrix as a polynomial relationship, i.e.:

Note: A, B, C respectively represent a polynomial

A polynomial corresponds to an R1CS matrix constraint that corresponds to the problem we want to prove. Based on the above conversion, we can know that if the polynomials satisfy the above relationship, it means that our R1CS matrix is correct, thus indicating that the prover’s secret input in the arithmetic circuit is also correct.

So our problem is simplified to: the verifier randomly chooses a number x and asks the prover to prove that A(x) * B(x)=C(x) is true. If it is true, it means that the prover’s secret input is correct.

Conversion between polynomials

In a complex arithmetic circuit, there are thousands of gates, and we need to verify whether each gate satisfies the R1CS constraint. In other words, we need to verify the equation A(x) * B(x)=C(x) several times to ensure its correctness. However, the efficiency of verifying them one by one is too low. How can we verify the correctness of all gate constraints at once?

For ease of understanding, we introduce a P(x) and let P(x) = A(x) * B(x) – C(x).

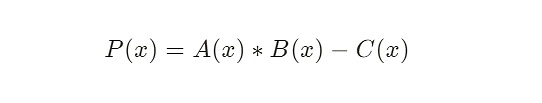
We know that any polynomial, as long as it has a solution, can be decomposed into a linear polynomial. Therefore, we split P(x) into F(x) and H(x), that is:

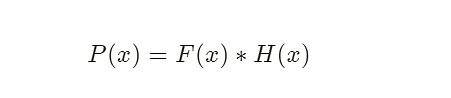
Then, F(x) is made public, which means that there exists H(x) = P(x)/F(x), so the polynomial we need to verify is finally transformed into:

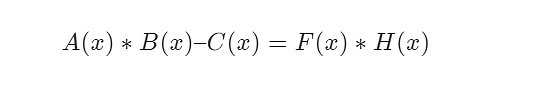
A(x) * B(x) – C(x): contains the coefficients of the polynomial, only known to the prover, i.e. secret input.

F(x): a public polynomial known to both the verifier and the prover, i.e. public input.

H(x): the prover knows it by calculation, and the verifier cannot know it.

And the final problem to be proved is: the polynomial equation A(x) * B(x) – C(x) = F(x) * H(x) holds for all x.

Now, we only need to verify the polynomial once to verify whether all constraints satisfy the matrix relationship.

So far, we have completed the process of transforming the problem to be proved into a polynomial that only needs to be verified once, thus achieving the simplicity of the system.

However, does this simplicity in verification time come at the expense of proof size?

In short, the proof protocol uses the structure of Merkle tree, which effectively reduces the size of the proof.

After the entire transformation process is completed, naturally two questions arise:

• Why transform into a polynomial?

  Because polynomials achieve the simplicity of proof. The problem with zero-knowledge proof is to verify that the calculation satisfies multiple constraints, and polynomials can verify multiple constraints with one point. In other words, the verifier originally had to verify the problem n times to confirm the correctness of the proof, but now only needs to verify once to greatly confirm the correctness of the proof.

• Why can verifying one point on the polynomial determine that the two polynomials A(x) * B(x) – C(x) = F(x) * H(x) hold?

  This is determined by the characteristics of polynomials, that is, the calculation result of a polynomial at any point can be regarded as the unique representation of its identity. For two polynomials, they only intersect at a limited number of points.

For the above two d-order polynomials: A(x) * B(x) – C(x) and F(x) * H(x), if they are not equal, they will intersect at most d points, that is, the solutions at d points are the same.

After the polynomial conversion is completed, we will enter the polynomial proof stage.

Prove the polynomial is valid

For convenience of explanation, we adopt polynomial P(x) = F(x) * H(x).

Now, the problem the prover wants to prove is: for all x, P(x) = F(x) * H(x).

The verification process of the above polynomial by the prover and the verifier is as follows:

• The verifier selects a random challenge point x and assumes x = s;

• After receiving s, the prover calculates P(s) and H(s) and gives these two values to the verifier;

• The verifier first calculates F(s), then calculates F(s) * H(s), and judges whether F(s) * H(s) = P(s) holds. If it does, the verification passes.

However, we will find that there are some problems with the above process upon careful consideration:

• The prover can know the information of the whole equation. If he receives a random point s, he can calculate F(s) and then construct a pair of false P(x) and H(x), so that P(s) = F(s) * H(s) to deceive the verifier.

• The prover does not use the s provided by the verifier to calculate F(s) and H(s), but uses other values to deceive the verifier.

• The value received by the verifier is calculated by the public input and the private input of the prover. If the verifier has great computing power, he can crack the prover’s private input.

For the above problems, we make the following optimizations:

• After the verifier selects a random point s, he homomorphically encrypts s. Homomorphic encryption means that the encrypted solution after calculation is equal to the solution after encryption. Under this encryption form, the prover can calculate the solution, but cannot construct false P(x) and H(x).

• When the verifier selects the challenge point s, he selects an additional random parameter λ and generates a linear relationship between s and λ. The verifier sends the homomorphically encrypted s and λ to the prover. After the prover sends the proof back, the verifier not only verifies whether the proof is true, but also verifies the relationship between the random parameter λ and s.

• To address the problem that the verifier can crack the secret input, we can introduce ZK. Throughout the entire proof, we can find that the prover only sends the calculated values of the polynomial to the verifier. The verifier can derive the coefficients of the polynomial from the values, i.e., the prover’s secret input. In order to prevent the verifier from deducing, when deriving the polynomials A, B, and C from R1CS, we can select two random numbers and add a set of values. This way, the restored polynomial has one additional order than the original polynomial, making it impossible for the verifier to obtain the information of the original polynomial from the encrypted polynomial, thus achieving ZK.

After optimization, we found that the proof system still requires interaction between the verifier and the prover. How can we achieve non-interaction?

Achieving Non-Interaction

To achieve non-interaction, SNARK introduces a trusted setup.

In other words, before the proof begins, the power of selecting random challenge points, which originally belonged to the verifier, is transferred to a trusted third party. After the third party selects a random parameter λ, the encrypted λ is placed in the R1CS circuit to generate the CRS (Common Reference String). The verifier can obtain their own Sv from the CRS, while the prover can obtain their own Sp from the CRS.

It should be noted that after generating Sv and Sp, λ needs to be destroyed. If λ is leaked, it may be used to forge transactions through false verification.

zk-SNARK Workflow

After understanding the construction process of SNARK, based on the arithmetic circuit we constructed, the proof process of zk-SNARK is as follows:

• Setup: (C circuit, λ) = (Sv, Sp)

  Generate random parameters Sv and Sp for subsequent provers and verifiers using circuit C and random parameter λ.

• Prove(Sp, x, w) = Π

  The prover calculates the proof Π through the random parameter Sp, the public input x, and the secret input w.

• Verify(Sv, x, Π) == (∃ w s.t. C(x,w))

  The verifier verifies whether C(x,w) = 0 exists through the random parameter Sv, public input x, and proof Π. At the same time, verify whether the proof is calculated through circuit C.

At this point, we have completed the explanation of the entire zk-SNARK. Now let’s take a look at a practical application case.

Case: Using Scroll’s zk Rollup as an Example

The role of the proof system is to convince the verifier to believe something;

For the zk proof system, it is to make the verifier believe that the Zero-Knowledge Proof calculated by the zk algorithm is true.

We use Scroll’s zk Rollup as an example to illustrate the operation of the zk proof system.

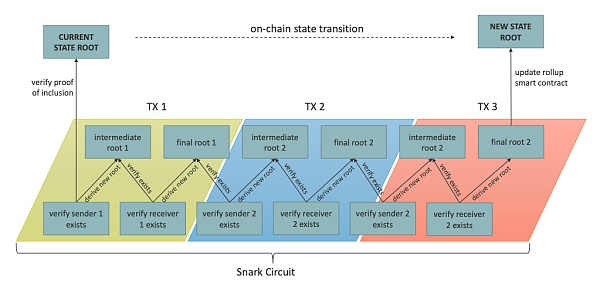
Rollup refers to off-chain calculation and on-chain verification. For zk Rollup, after the transaction is executed off-chain, the prover needs to generate a zk proof for the new state root generated after the transaction is executed, and then transfer the proof to the L1 Rollup contract for on-chain verification.

It should be noted that there are two types of blocks in zk Rollup:

• L1 Rollup Block: Blocks submitted to Ethereum

• L2 Block: Blocks composed of transactions submitted by users on L2

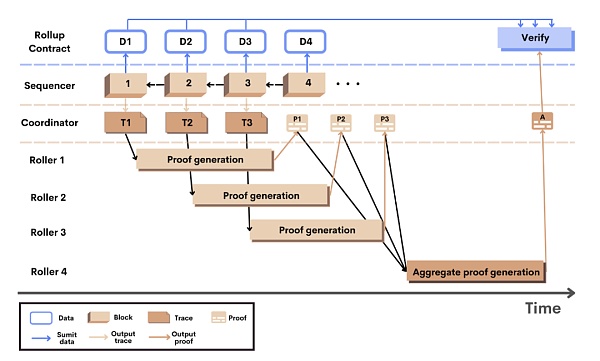
The following is the workflow of Scroll’s zk Rollup:

• The user initiates a transaction on L2, and the Sequencer retrieves the transaction, executes the transaction off-chain, generates an L2 block and a new state root; at the same time, submits the transaction data and new state root to the Rollup contract on Ethereum (submitting transaction data is to achieve data availability);

• When the L2 block is generated, the Coordinator will receive the execution trajectory of the block from the Sequencer, and then randomly assign the trajectory to any Roller;

• The Roller converts the received execution trajectory into a circuit, and generates a validity proof for each circuit, and then sends the proof back to the Coordinator;

• When k L2 blocks are generated, the Coordinator sends an aggregation task to another Roller to aggregate the proofs of the k blocks into a single aggregate proof;

• The Coordinator submits the single aggregate proof to the Rollup contract. The Rollup contract verifies the aggregate proof together with the previously submitted state root and transaction data. If the verification passes, the corresponding block is considered to be finally confirmed on Scroll.

From the above process, it can be seen that the Roller is the prover in the system, and the Rollup contract is the verifier. The Roller generates a zk proof for the off-chain executed transaction; the Rollup contract verifies the proof. If the verification passes, the Rollup contract will directly adopt the submitted state root as its new state root.

We will continue to update Blocking; if you have any questions or suggestions, please contact us!