An Introduction to Fully Homomorphic Encryption Definition and Historical Review

Introduction to Fully Homomorphic Encryption

Author: Steven Yue

A while ago, I took the CS355 (Advanced Cryptography) course at Stanford. The course was taught by three PhD students of Dan, Dima Kogan, Florian Tramer, and Saba Eskandarian. Each of the three PhD instructors has their own characteristics and research directions. Dima focuses on privacy-preserving technology PIR (Private Information Retrieval), Florian focuses on ML and blockchain research, and Saba focuses on zero-knowledge proofs.

CS355 covers almost all aspects of cryptography from ancient to modern times. From the earliest one-way functions, to elliptic curves (ECC) and LianGuaiiring, and finally to some hot topics in recent years such as MPC, zero-knowledge, private information retrieval (PIR), fully homomorphic algorithms, and so on. As the course just ended a few days ago, I took the opportunity to organize my notes while the knowledge is still fresh in my memory. The course content is very interesting, and I will share more content with you in the future when I have time~

In this issue, let’s talk about the recently popular fully homomorphic encryption (FHE) and the accompanying lattice-based encryption technology.

• friend.tech user falls victim to SIM Swap attack. Is Verizon’s SMS verification a security vulnerability?
• Sequoia Capital The challenging moment has arrived, how should we prepare?
• What are long positions and short positions?

What is Fully Homomorphic Encryption

I believe many friends have heard of the name of fully homomorphic encryption (FHE) to some extent. In recent years, there have been more and more discussions on personal privacy protection, and a series of cryptographic application technologies including homomorphic encryption have been widely popularized.

In order to better understand this topic, I would like to briefly introduce the definition of fully homomorphic encryption.

Review of Encryption Systems

Before we start, let’s review the most traditional encryption systems.

We all know that to construct an encryption system, we often need a key. With this key, we can encrypt the plaintext into ciphertext, and then decrypt the ciphertext back to its original form using the key. Without this key, it is difficult for others to know what information we have transmitted.

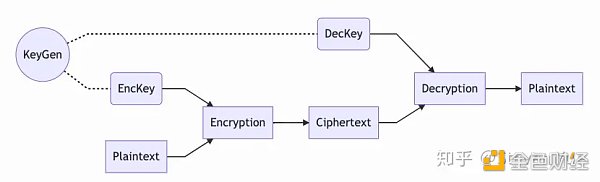
The above figure basically shows the overview of all common encryption systems. All encryption systems, if described in a more formal way, undoubtedly do three things:

Friends who are familiar with encryption algorithms will surely know some common encryption algorithms such as AES, RSA, etc. You will also know that encryption systems are generally divided into two types: symmetric encryption systems and asymmetric encryption systems. The three steps described here are actually applicable to any encryption system. If it is symmetric, the key used for encryption and decryption is the same. If it is an asymmetric system, the encryption uses a public key, and the decryption uses a different private key.

In cryptographic research, whenever we see the definition of a new system, we often need to state the properties that this system should have.

The main significance of semantic security is that onlookers cannot distinguish between two encrypted messages. So if an intruder eavesdrops on the network and sees the encrypted information I send, as long as the encryption system I use is semantically secure, I can be sure that the intruder cannot obtain any information about the encrypted content from the ciphertext.

After meeting the above two properties, an encryption system becomes sound.

Homomorphic Encryption: An accidental special property

After understanding how encryption systems work, let’s take a closer look at this seemingly random gibberish ciphertext. We all know that just by looking at the ciphertext itself, we won’t get any information. But does this mean that if we don’t have the key and only have the ciphertext, we can’t do anything?

The answer is that we all know: actually, it’s not true.

For this property, we call it additive homomorphism. It means that the ciphertext after encryption maintains a subtle algebraic relationship with the original plaintext. If we add up the ciphertexts, we can obtain a new ciphertext that represents the sum of the original plaintexts. Similarly, there exist encryption algorithms that have multiplicative homomorphism in addition to additive homomorphism. With a multiplication homomorphic algorithm, we can multiply the ciphertexts together and obtain a ciphertext that corresponds to the result of multiplying the original plaintexts. Throughout this process, we don’t need to know any information related to the key, we simply combine the seemingly random gibberish ciphertexts.

An Example: Anonymous Voting System

Next, let’s take an example to vividly describe the practicality of homomorphic encryption.

We all know how online voting works – suppose a company’s boss wants to initiate a vote to decide whether the company should adopt a 996 work schedule. The boss can have the IT department set up a server for employees to submit their choices: vote 0 means no, vote 1 means yes. After the voting phase ends, the boss can add up all the votes. If the total number of votes exceeds half the number of employees, the company will start implementing the 996 schedule.

This voting mechanism seems simple, but there is a big privacy issue: suppose the boss secretly wants everyone to work 996, but just initiates this vote as a fishing expedition to see which employees are unwilling to work overtime. In this case, the boss can secretly instruct their subordinates to eavesdrop on the network and record the choices of each employee, ultimately revealing who voted 0. This makes employees very afraid and unwilling to express their true opinions.

If we can use an encryption algorithm with additive homomorphism, then this problem can be easily solved.

Of course, this system is still very incomplete. For example, the IT department can directly help the boss decrypt each person’s vote and record it as a document. There are other cryptographic tools that can help us solve this problem. Due to space constraints, I won’t go into further detail here.

However, at this point, we should be able to feel the power of homomorphic encryption algorithms. We can understand it in this way: through homomorphic encryption algorithms, users can perform secure delegated computation with an untrusted remote server (cloud). Users can encrypt their sensitive privacy inputs using homomorphic encryption technology and entrust them to the cloud. The cloud can then perform a certain degree of computation on the encrypted data, and finally obtain the desired encrypted results and return them to the user. Finally, the user can use the decryption key to open the obtained results. Throughout the protocol, the delegate (cloud) cannot see any useful information related to private inputs.

Classification of Homomorphic Encryption Systems

After a rough understanding of the two most basic homomorphic properties, other concepts become very easy to understand. If we look at the system as a whole, homomorphic encryption systems can be roughly divided into four categories: partially homomorphic, somewhat homomorphic, limited series fully homomorphic, and fully homomorphic.

Next, let’s take a look at the specific definitions of each category one by one.

Partially Homomorphic Encryption (LianGuairtially Homomorphic Encryption)

The most basic stage of homomorphic encryption is called partially homomorphic encryption, where the ciphertext has only one homomorphic property. This stage includes the two modes of homomorphic addition and homomorphic multiplication described earlier.

We obtain the ciphertext corresponding to the multiplication of these two messages! This is the property of homomorphic multiplication, and we can continue to stack new ciphertexts on top of this ciphertext, so that we can obtain arbitrary multiplications between ciphertexts.

Somewhat Homomorphic Encryption

As we mentioned in the previous paragraph, if we want to multiply private inputs and obtain their linear combinations, pure partially homomorphic encryption algorithms (RSA, ElGamal) cannot achieve this. So we need to move on to the next stage.

The next stage of partially homomorphic encryption is somewhat homomorphic encryption, which is a step closer to the fully homomorphic encryption we want to achieve. If we have a somewhat homomorphic encryption algorithm, we can perform both addition and multiplication on the ciphertext. However, it should be noted that because this stage is somewhat homomorphic, the number of additions and multiplications that can be done is very limited, and the function F that can be computed is also limited within a finite range.

There are not many common examples of somewhat homomorphic encryption. If we have to mention the most easily understood example, it should be the cyclic group encryption algorithm based on pairings (LianGuaiiring).

In the previous discussion, we briefly discussed the ElGamal encryption algorithm based on an ordinary cyclic group. We all know that this algorithm is homomorphic with addition, that is, we can obtain linear combinations of arbitrary ciphertexts. In fact, in certain special cyclic groups, we can also find some weak homomorphic properties with multiplication.

This limitation demonstrates that the system is approximately homomorphic because we cannot compute any arbitrary logic and deep function F.

Fully Leveled Homomorphic Encryption

After reaching the next stage, we are one step closer to the goal of fully homomorphic encryption.

This stage is called fully leveled homomorphic encryption. In this stage, we can perform arbitrary combinations of addition and multiplication on ciphertext without any limitations on the degree.

Fully Homomorphic Encryption (FHE)

After countless requests, we finally come to the eagerly awaited fully homomorphic encryption (FHE).

As the name suggests, a fully homomorphic encryption system has no restrictions on any computational methods. We can combine ciphertexts arbitrarily without the need for a key, creating new ciphertexts that can be perfectly decrypted regardless of the computational complexity.

When we reach this stage, secure proxy computation, mentioned earlier, becomes feasible. If we can find an efficient fully homomorphic encryption system, we can securely delegate all local computations to the cloud without leaking any data!

Definition of a Fully Homomorphic Encryption System

Before delving into the history of fully homomorphic encryption, let’s systematically define the formal definition of a fully homomorphic system. A fully homomorphic encryption system consists of four algorithms:

A Review of the History of Fully Homomorphic Encryption

Before diving into how fully homomorphic encryption algorithms are implemented, let’s take a look at the origin of the concept of fully homomorphic encryption.

The concept of FHE (fully homomorphic encryption) was actually proposed in the late 1970s. In 1978, several cryptography experts, Rivest, Adleman, and Dertouzos, first mentioned the idea of performing calculations on ciphertexts to indirectly operate on plaintexts in their paper “On Data Banks and Privacy Homomorphisms.” Later, this idea was summarized and named fully homomorphic encryption.

It can be seen that the concept of fully homomorphic encryption has been around for a long time. Surprisingly, in 1976, two years before the publication of the paper, the Diffie-Hellman key exchange protocol was just proposed! This shows the rich imagination of cryptography experts.

After the concept of FHE was introduced, the entire academic community was intrigued and embarked on a decades-long search to find a perfect algorithm with fully homomorphic properties. However, after these decades, people have tried every possible option but have not found one that satisfies all the conditions for fully homomorphic encryption and whose security can be easily verified.

It was not until 2009 that Craig Gentry, a PhD student at Stanford, had a sudden inspiration and broke through the difficulty of FHE algorithm. In his doctoral thesis, he first proposed a reasonable and secure fully homomorphic encryption system! This system is based on the assumption of ideal lattice. The fully homomorphic system proposed by Gentry09 is often referred to as the first generation fully homomorphic encryption system.

In Gentry’s paper, he also mentioned a crucial concept called Bootstrapping. Bootstrapping is a special processing technique for ciphertext, which can “refresh” a ciphertext with noise close to the critical value into a new ciphertext with very low noise. Through Bootstrapping, the noise of a finite level system can never exceed the critical value, thus becoming a fully homomorphic system. In this way, we can homomorphically compute any size of F.

After Gentry’s breakthrough, the entire cryptography community once again went crazy, and everyone began to search for more efficient and versatile fully homomorphic systems based on Gentry’s ideas.

In 2011, two giants, Brakerski and Vaikuntanathan, proposed a new fully homomorphic encryption system based on another assumption of lattice encryption called Learning With Errors (LWE). In the same year, Brakerski, Gentry, and Vaikuntanathan completed and officially published this system together. The fully homomorphic system they invented is called the BGV system. The BGV system is a finite level homomorphic encryption system, but it can be transformed into a fully homomorphic system through Bootstrapping. Compared with the system proposed by Gentry09, the BGV system uses a more practical LWE assumption. Generally, we refer to the BGV system as the second generation fully homomorphic encryption system.

In 2013, Gentry returned again. Gentry, Sahai, and Waters introduced the new GSW fully homomorphic encryption system. The GSW system is similar to BGV, with finite level fully homomorphic properties itself, based on a simpler LWE assumption, and can achieve fully homomorphic encryption through Bootstrapping. We generally refer to the GSW system as the third generation fully homomorphic encryption system.

After 2013, the cryptography community has become extremely diverse. On top of the three generations of fully homomorphic systems, various new designs have emerged, dedicated to optimizing and accelerating the operation efficiency of BGV and GSW systems. IBM developed an open-source fully homomorphic computation library, HElib, based on the BGV system, and successfully ported it to major mobile platforms. At the same time, another open-source project, TFHE, is also worth noting. TFHE is based on the GSW system, with various optimizations and accelerations, and is now very famous.

In addition to developing traditional fully homomorphic libraries, many teams are also researching how to better accelerate the computation of fully homomorphic encryption algorithms through heterogeneous hardware such as GPUs, FPGAs, and ASICs. For example, cuFHE is a well-known GPU-accelerated fully homomorphic encryption system based on CUDA.

From today’s perspective, looking back, it has been 11 years since Gentry opened the door to the field of fully homomorphic encryption. Now, the research on FHE in the industry is diverse, and many people are studying fully homomorphic systems from different perspectives and application requirements. Until today, we already have multiple feasible implementations of FHE, but what people are constantly pursuing now is the efficiency of FHE system operation. Taking the most advanced FHE library as an example, it may take tens of milliseconds or even tens of seconds to perform homomorphic computation of relatively simple logic on a mobile platform. These time units are extremely slow for computer systems.

How to make the FHE system more efficient on heterogeneous platforms is still a mystery. Once this problem is solved, it will be easy to turn all computer calculations into fully homomorphic ones and have them computed by a third-party cloud agent.

The Relationship Between FHE and MPC

Before concluding this article, I would like to explain the relationship between FHE and MPC. MPC stands for Secure Multi-Party Computation, which refers to the scenario where multiple parties have their own private inputs that they do not want to disclose to others, but they want to collectively compute a function F and share the computed result.

MPC is already a well-known and extensively researched field. Since the cryptographic researcher Andrew Yao introduced his Garbled Circuits in the last century, MPC has gained wide recognition and made many breakthroughs. We now have many usable MPC libraries that also offer certain operational efficiency.

If someone familiar with MPC reads about the arduous history of fully homomorphic encryption systems, they may wonder why we cannot simply replace fully homomorphic encryption with an MPC protocol.

Indeed, an MPC protocol can completely replace an FHE protocol. We only need to treat the users and their private inputs as one party in the protocol, and the remote computing server as another party. This satisfies the conditions for executing an MPC protocol, and by means of certain interactions, we can achieve proxy computation without the server being able to see the private inputs.

However, there is an important point that we have overlooked: since MPC involves interaction, it requires the users and the server to jointly compute and communicate in order to complete the protocol. This fundamentally conflicts with the underlying requirement of FHE proxy computation. If the user needs to stay online to complete the protocol and also contribute some computational power, then the computation is not actually being “proxied”. Both parties are simply performing more computations for the sake of information security. This also explains why the field of MPC has made significant breakthroughs while the field of FHE remains largely unknown, as the two systems solve completely different problems.

Next Stop: GSW Fully Homomorphic Encryption System

By now, I believe everyone has a thorough understanding of fully homomorphic encryption systems.

Next, let’s learn about the GSW fully homomorphic encryption system mentioned earlier in this article. Although it is considered the third generation of fully homomorphic systems, I believe GSW is the system that requires the fewest assumptions, has the simplest construction, and is the easiest to understand. There are also many open-source libraries (such as TFHE) based on the GSW system.

Due to the length of this article, we will conclude here. In the next article, we can start by learning the basics of the GSW system: lattice-based encryption schemes and the LWE problem. Once we understand the LWE problem, the problems that GSW solves will become very clear.

We will continue to update Blocking; if you have any questions or suggestions, please contact us!