Homomorphic Encryption Research What Changes Will it Bring to Web3 without the Need for Decryption?

Homomorphic Encryption Research Impact on Web3 without Decryption

As the market remains quiet in the bear market, investors and project parties always start looking for new growth points.

In the window period lacking sustained hotspots, it is an excellent opportunity to explore and deeply understand new technologies, as new technologies may become the core of the next market narrative.

Last month, well-known crypto venture capital firm Portal Ventures published a detailed article on its official blog discussing the technology of Fully Homomorphic Encryption (FHE). However, this in-depth technical article seems to have not attracted widespread attention from the public.

• CYBER token surged after the DWF action.
• Besides Unibot, what other potential new Telegram Bots are worth paying attention to?
• LD Capital After Friend.tech, how will Base ecosystem continue?

The author of Portal Ventures said, “Fully Homomorphic Encryption is the holy grail of encryption schemes.”

Understanding the technologies that venture capitalists focus on is crucial for investors because it can help us predict and understand potential trends in the next market cycle. In fact, technologies such as homomorphic encryption, zero-knowledge proofs, and multi-party secure computation have profound implications in the field of cryptography, especially Fully Homomorphic Encryption, which may have huge application potential in the cryptocurrency and web3 domains.

But the problem is that most people know very little about the true meaning of Fully Homomorphic Encryption, how it works, and how it differs from other technologies. In a sluggish market with low investment sentiment, it is undoubtedly a wise choice to step out of the hype and delve into the research and understanding of these cutting-edge technologies.

It is somewhat coincidental that years ago, I had the opportunity to work with FHE-related technological solutions. Therefore, I decided to delve into this article by Portal Ventures and provide some new perspectives and thoughts.

What are homomorphism and Fully Homomorphic Encryption?

If you directly read the original article by Portal Ventures, you may find the complex mathematical description of Fully Homomorphic Encryption (FHE) confusing.

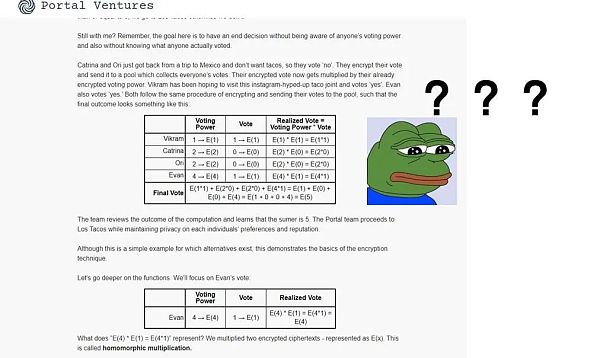
In fact, the world of cryptography is full of depth and technicality, but we can completely explain these concepts in simple and popular ways. In this section, I will try to provide you with some more intuitive and easy-to-understand examples to help you gain a deeper understanding of Fully Homomorphic Encryption.

First, imagine a “secret magic box.” You can put any item into this box and lock it. Once locked, you cannot see or touch the contents of the box. However, surprisingly, this magic box allows you to change the color or shape of the items inside without opening it.

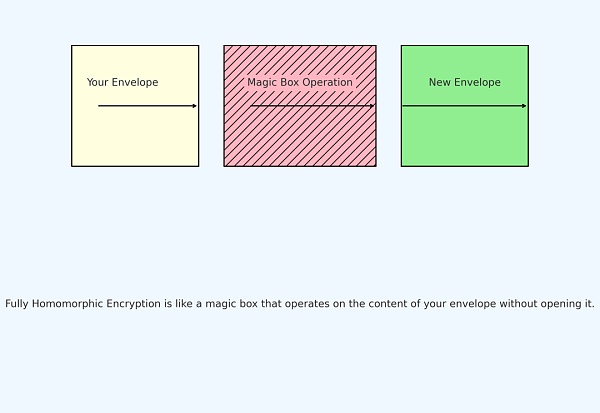
As shown in the above figure, Fully Homomorphic Encryption (FHE) can be seen as a magic box:

1. Your Envelope: This represents the original data you want to encrypt.

2. Magic Box Operation: Even without decrypting or opening the envelope, you can perform operations (such as addition, subtraction, etc.) on the data inside the envelope.

3. New Envelope: After the magic box operation, you will get a new encrypted result.

This is the basic idea of homomorphic encryption: being able to manipulate encrypted data without understanding the data itself.

This simple example helps to understand what “fully homomorphic encryption” is doing. But in reality, this concept itself is a bit like listening to a word from the emperor. So, what does “fully” and “homomorphic” mean?

1. What does “fully” mean?

• In cryptography, encryption schemes can support various operations, such as addition, multiplication, etc. When we say an encryption scheme is “fully homomorphic,” we mean that this encryption scheme supports an arbitrary number of basic operations (such as addition and multiplication) on encrypted data without the need for decryption. This is in contrast to partially homomorphic encryption schemes (such as schemes that only support addition or multiplication).

2. What does “homomorphic” mean?

• “Homomorphic” comes from Greek and means “same shape or structure.” In cryptography, when we say an encryption scheme is homomorphic, it means that some operations have the same effect on plaintext as they do on ciphertext. In other words, if you perform a certain operation on encrypted data and then decrypt the result, it is equivalent to decrypting the data first and then performing the same operation on the decrypted data.

3. For example, consider an encryption scheme that supports homomorphic addition. Suppose you have two numbers: 3 and 4. You can encrypt these two numbers first and then use this homomorphic encryption scheme to add the two encrypted numbers. Finally, you decrypt the result of the addition. The decrypted result will be 7, which is the same as the result you would get by simply adding 3 and 4 in plaintext.

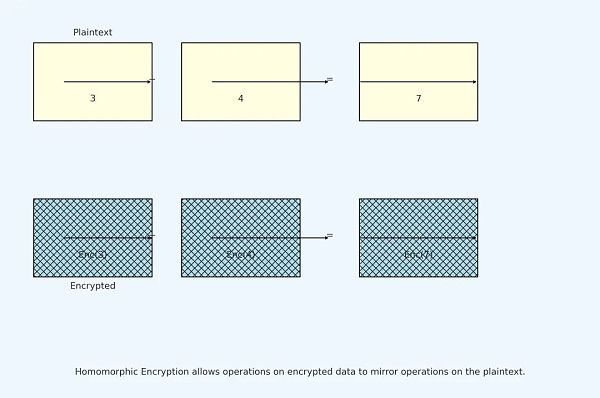
However, you may wonder how we can perform these addition, subtraction, multiplication, and division operations on non-numeric data. In fact, we can use specific encoding methods to convert non-numeric data into numeric form, so that we can perform addition, multiplication, and other operations on them. This means that the application of fully homomorphic encryption is not limited to mathematical calculations, but can also be widely used in other fields.

To explain this concept more intuitively, let’s consider an example of medical data.

1. Suppose a hospital has some patient data, such as age and blood sugar level, but they do not want to send this data directly to a cloud service provider for analysis due to privacy concerns.

2. By using fully homomorphic encryption, the hospital can encrypt this data first.

3. Imagine that the cloud service provider needs to calculate the average age of all patients (which requires addition and division) and the product of the sum of blood sugar levels and the number of patients (which involves addition and multiplication).

4. All these calculations can be performed on the encrypted data without decryption. The cloud service provider performs the calculations without decrypting the data and then returns the encrypted results to the hospital. This ensures the privacy of the data while meeting the data processing needs.

This is the charm of fully homomorphic encryption, which provides us with a secure and flexible method of data processing.

Why is FHE important?

Currently, existing methods for computing encrypted data are not ideal. They are relatively expensive in terms of resource usage and time consumption.

Therefore, the industry standard process is to have a third party (i.e. a company) decrypt the data before performing computations.

To illustrate with a specific example, imagine you have a data file containing financial information about high-profile individuals.

• We call this file “M”. We need a company to analyze this data.

• What is the current process? First, I encrypt M using encryption functions like RSA or AES. At this point, M becomes E(M), where E is the encryption function.

• Next, I send E(M) to the company’s server. The company then decrypts E(M) into plaintext using the corresponding decryption function D, resulting in D(M).

• The company directly performs analysis operations on the plaintext file M.

• After the operations are completed, M is encrypted again to generate E(M’).

• The company sends the encrypted M’ back to me, and then I decrypt it again.

Do you notice the key issue here? When the company decrypts M and stores it on its server for computation, a third party can access the originally protected sensitive data. This can lead to problems if this person is attacked by hackers or has malicious intent.

Fully homomorphic encryption (FHE) solves this problem by allowing computations on encrypted data. The company no longer needs to decrypt E(M). It can perform analysis directly on the encrypted data. There is no need for decryption or trust assumptions.

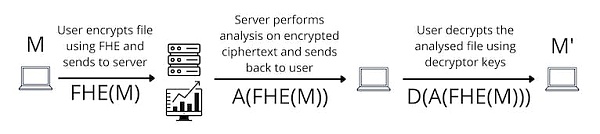
In summary, the introduction of fully homomorphic encryption resolves a key issue in the current data processing workflow, which is the privacy risk that may be exposed when a third party handles the data. FHE provides us with an effective method of processing encrypted data while ensuring data privacy.

How is FHE applied in cryptography?

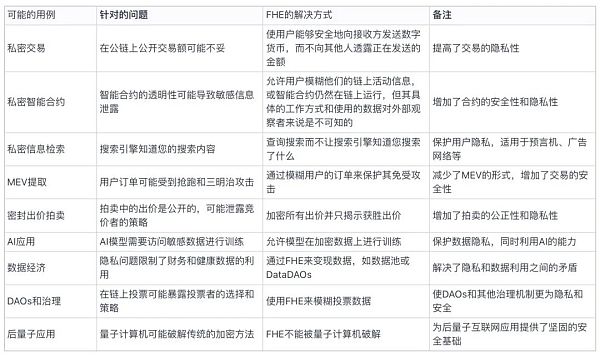
Fully homomorphic encryption (FHE) opens a new door for the world of encryption and brings us many previously unimaginable application scenarios. The original article by Poly Venture provides a simple description of these scenarios, and we have attempted to present a more organized interpretation in the form of a table.

FHE vs ZK vs MPC, can’t tell them apart?

After understanding fully homomorphic encryption (FHE), it is easy to compare it to other familiar technologies such as zero-knowledge proofs (ZK) and multi-party computation (MPC). At first glance, they all seem to be dedicated to addressing similar privacy and computation problems. But what are the actual connections and differences between these three?

First, let’s have a basic understanding of the definitions of these three technologies:

• FHE: Allows computations to be performed on encrypted data without the need for decryption.

• ZK: Allows one party to prove to another party that a statement is true without revealing any specific information about that statement.

• MPC: Enables multiple parties to jointly perform computations on their private data without revealing input data to other participants.

Now, let’s look at their similarities and differences from multiple dimensions:

1. Objectives:

• The main objective of FHE is to perform computations without decryption.

• The goal of ZK is to prove the correctness of a fact without revealing any information about that fact.

• The objective of MPC is to allow multiple parties to compute together securely without revealing their respective inputs.

2. Privacy and Computation:

• In ZK, computation is not necessarily private. For example, although you can use ZK to verify if a bank account balance exceeds $100,000, the computation for such verification is not necessarily private.

• In contrast, FHE ensures the privacy of computations since all computations are performed on encrypted data.

3. Limitations and Challenges:

• MPC requires at least one honest server and may be affected by DDoS attacks, collusion attacks, and communication overhead.

• ZK is primarily used for proving correctness rather than privacy technologies.

• Although FHE provides strong privacy, its computation efficiency is low and it requires significant resources.

4. Applications in the field of encryption:

• FHE can be used to build more private smart contracts and other blockchain applications.

• ZK is used to create scalable blockchain solutions, such as zk-rollups.

• MPC is mainly used for private key management and custody.

5. Cross-usage:

• MPC can be combined with FHE to form threshold FHE, enhancing security by splitting an FHE encryption key into multiple parts and giving each participant one part.

• zkFHE is a combination of zero-knowledge proof and fully homomorphic encryption. It is being researched to achieve zk-rollups on FHE smart contracts.

Overall, although FHE, ZK, and MPC overlap in certain aspects, they each have their unique advantages and application scenarios. In the world of encryption, these three technologies offer great potential for enhancing privacy and security, but their combination and further research remain an active area in the crypto community.

Finally, we can also provide a brief comparison table to visually understand these technologies together.

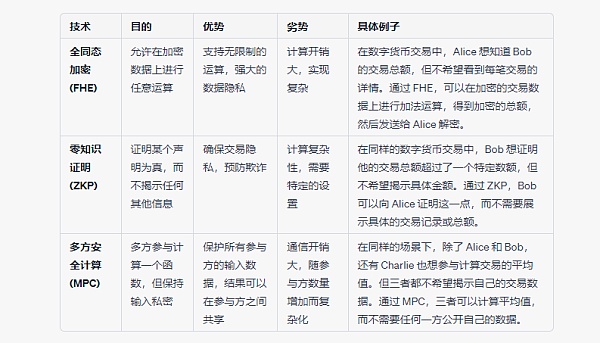
Future Prospects of FHE

Through the above text, it is clear that Fully Homomorphic Encryption (FHE) is a powerful technology.

But why hasn’t it been widely adopted, and why is it rarely mentioned in the field of encrypted CT? On one hand, understanding the technology itself requires a certain level of expertise. On the other hand, FHE technology currently faces some challenges, making it difficult to easily enter the public’s view in a commercialized form.

The challenges faced may include:

1. Computational Intensity: When our ciphertexts interact with each other, more noise is added to maintain security. FHE schemes use “bootstrapping” techniques to reduce noise, but this is computationally intensive and resource-consuming.

2. Limited Functionality: FHE computations are limited to addition, multiplication, and their variations/combinations. For example, if statements cannot be used in FHE because the content is encrypted. Additionally, building complex operations such as comparison and division requires careful planning of basic logic, leading to more complex programming techniques and lower computational efficiency.

3. Compatibility/Composition Issues: Existing applications and service providers are not built for computations on encrypted data. This limits the integration of FHE with existing technologies and adds inertia to developing FHE-compatible applications.

Possible solutions:

1. Hardware Accelerators: Certain FHE schemes, such as nuFHE and cuFHE, can utilize GPU acceleration, but the main breakthrough will come from faster FPGA and ASIC. Other technologies, such as photonics, are also being researched to accelerate hardware use cases for FHE.

2. New Programming Paradigms: Just as packages like LianGuaindas and numpy are used for complex mathematics in Python, FHE libraries will also be built. Currently, Zama and Sunscreen are two projects building such libraries and SDKs for FHE. Additionally, dedicated compilers need to be built to allow developers to unify FHE, ZKP, and MPC.

3. Integration with Existing Solutions: Solutions will be built to make existing tools compatible with FHE as an intermediate layer between tools and FHE-encrypted data.

Finally, in the conclusion section, Portal Ventures emphasizes again:

“FHE is the holy grail of computation, and we are getting close to its commercialization. Value and computation are transitioning to open, permissionless networks, and we believe FHE will underpin much of the necessary infrastructure and applications.”

Furthermore, they also express interest in projects currently researching FHE. Therefore, what we can see is that VCs are interested in FHE, or VCs will be the first to be interested in hardcore technologies that have not yet entered the mainstream.

History has shown that encryption projects based on new technologies often have a shining halo and higher valuations, and are sought after by various capital sources.

Before the next feast begins, we should indeed spend more time researching the identities of the guests entering in advance in order to respond well when the banquet starts.

We will continue to update Blocking; if you have any questions or suggestions, please contact us!