Vitalik: In-depth Understanding of Cross-L2 Reading – What are the Cross-Chain Proof Solutions

Vitalik's Understanding of Cross-L2 Reading and Cross-Chain Proof Solutions

Author: Vitalik, Founder of Ethereum; Translator: Blockingcryptonaitive

In the article “Three Technical Transformations Needed for the Ethereum Ecosystem,” I outlined why it is necessary to consider L1+cross-L2 support, wallet security, and privacy as fundamental features of the Ethereum ecosystem stack, rather than as key add-ons that can be separately designed by individual wallets.

This article will more directly focus on the technical aspects of a specific sub-problem: making it easier to read from L1 to L2, read from L2 to L1, or read from one L2 to another L2. Solving this problem is crucial for implementing asset/key-store separation architecture, but it also has valuable uses in other areas, particularly optimizing reliable L2-to-L2 calls, including use cases such as transferring assets between L1 and L2.

Table of Contents:

• Why DeFi is Broken: The Importance of Non-Oracle Protocols
• CoinEx fined $1.7 million and reached a settlement with the New York State Attorney General’s Office (NYAG)
• Evolution of Uniswap: Opportunities and Impacts of V4

• What is the Goal?

• What Does Cross-Chain Proof Look Like?

• What Proof Schemes Can We Use?

• Merkle Proofs

• ZK SNARKs

• Special-Purpose KZG Proofs

• Verkle Tree Proofs

• Aggregation

• Direct State Reads

• How Does L2 Get the Latest Ethereum State Root?

• Not a Wallet on the L2 Chain

• Privacy

• Summary

What is the Goal?

Once L2s become more mainstream, users will have assets on multiple L2s and possibly L1s. Once smart contract wallets (multisig, social recovery, or other types) become mainstream, the keys required to access an account will change over time, and old keys will no longer be valid. Once both of these happen, users will need a way to change the keys that have permission to access many accounts located in many different places, without having to do a large number of transactions.

In particular, we need a way to handle “counterfactual addresses”: addresses that have not yet been “registered” on-chain in any way, but still need to receive and safeguard funds. We all rely on counterfactual addresses: when you first use Ethereum, you can generate an ETH address that others can use to send you funds without having to “register” the address on-chain (which would require paying transaction fees and thus holding some ETH).

For EOAs (external accounts), all addresses are initially counterfactual. For smart contract wallets, counterfactual addresses are still possible, primarily thanks to CREATE2, which lets you have an ETH address that can only be populated by a smart contract with code that matches a specific hash.

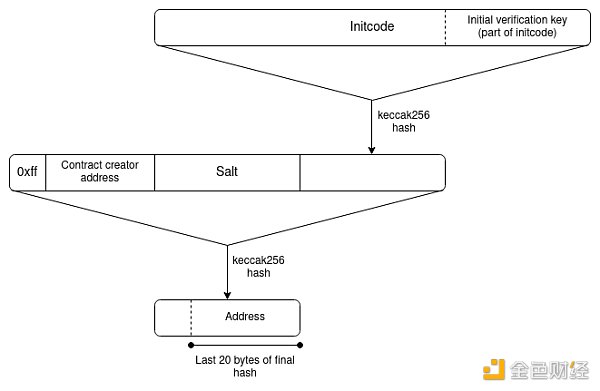
EIP-1014 (CREATE2) Address Computation Algorithm

However, smart contract wallets introduce a new challenge: access keys may change. The address (as the hash of the initcode) can only contain the wallet’s initial validation key. The current validation key will be stored in the wallet’s storage, but that storage record will not propagate automatically to other L2s.

If a user has many addresses on many L2s, including ones that the L2 in question doesn’t know about (because they are counterfactual), it seems that the only way for the user to change their keys is with an asset/key separation architecture. Each user has (i) a “keyring contract” (on L1 or a specific L2) that stores all the wallet’s validation keys and the rules for changing keys, and (ii) “wallet contracts” on L1 and many L2s that are used for cross-chain reads to obtain validation keys.

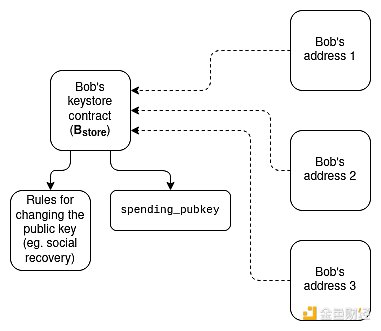
There are two implementation methods:

1. Lightweight version (checking only for key updates): Each wallet stores the validation key locally and contains a function that can be called to check a cross-chain proof of the current state from the keyring and update the locally stored validation key. Calling this function to get the current validation key from the keyring is necessary when using the wallet for the first time on a particular L2.

• Pros: Saves on the use of cross-chain proofs, so the expense of cross-chain proofs is not a concern. All funds can only be used with the current key, so it is still secure.

• Cons: To change the validation key, you must make on-chain key changes in the keyring and in every initialized wallet (though not counterfactual ones). This may require a large amount of gas fees.

2. Heavy version (checking on every transaction): Each transaction requires a cross-chain proof that proves the key is currently present in the key library.

• Pros: Lower system complexity and lower cost to update key library.

• Cons: Every transaction is expensive, so more engineering is needed to make the cost of cross-chain proof acceptable. Also, it is not easy to be compatible with ERC-4337 because ERC-4337 currently does not support cross-contract reads of mutable objects during validation.

What does a cross-chain proof look like?

To illustrate the full complexity, we will explore the most difficult case: the key library is on one L2 and the wallet is on another L2. If either the key library or the wallet is on L1, only half of this design is needed.

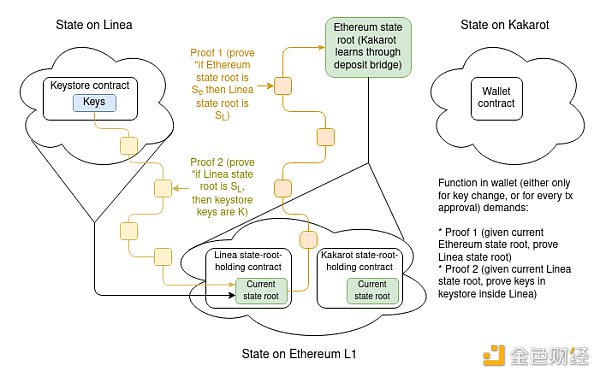Assuming the key library is on Linea and the wallet is on Kakarot, the complete wallet key proof includes:

• A proof that proves the current Linea state root based on the current Ethereum state root known by Kakarot.

• A proof that proves the current key in the key library based on the current Linea state root.

There are two main implementation issues here:

1. What kind of proof do we use? (Is it a Merkle proof? Or something else?)

2. How does L2 initially know the most recent L1 (Ethereum) state root (or, as we will see, it may be the full L1 state)? Conversely, how does L1 know the L2 state root?

• What happens on one side until the other side can prove something, and how long is the delay in between?

What proof schemes can we use?

There are five main choices:

• Merkle proof

• General-purpose ZK-SNARKs

• Special-purpose proof (e.g., using KZG)

• Verkle proof, which is between KZG and ZK-SNARKs and involves both infrastructure workload and cost.

• No proof, relying on direct state reads

Regarding the necessary infrastructure work and user costs, I roughly arranged them in the following order:

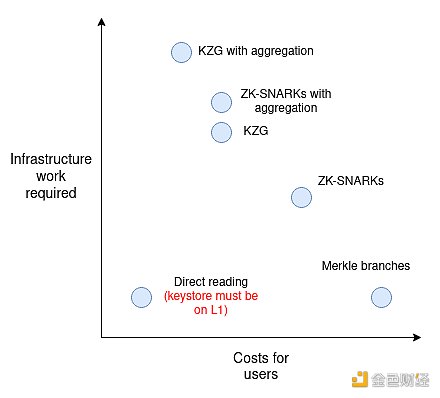
“Aggregation” refers to aggregating all proofs provided by users into one large proof per block, which is possible for SNARKs and KZG but not for Merkle branches (you can combine Merkle branches to a certain extent, but in practice, you can only save about log(number of transactions per block)/log(total number of keys in the keystore) of work, which may only be 15-30% in reality, so the cost may not be worth it).

Aggregation only becomes valuable when there are a large number of users in the system, so in the implementation of version 1, aggregation is skipped and then implemented in version 2.

How will Merkle proofs work?

This is quite simple: operate directly according to the chart in the previous section. More specifically, each “proof” (assuming the most difficult case of proving an L2 in an L2) will contain:

• A Merkle branch proving the state root of the L2 holding the keystore, according to the latest Ethereum state root known to the L2. The state root of the L2 holding the keystore is stored in a known storage slot at a known address (represented as a contract on L1 for L2), so the path can be hard-coded.

• A Merkle branch proving the current validation key according to the state root of the L2 holding the keystore. Here, the validation key is also stored in a known storage slot at a known address, so the path can be hard-coded.

Unfortunately, Ethereum state proofs are complex, but libraries exist for verifying them, so implementing this mechanism is not too complicated if using these libraries.

A bigger problem is cost. Merkle proofs are long, and the Blockingtricia tree unfortunately takes about 3.9 times the necessary length (precisely: the ideal Merkle proof length for a tree containing N objects is 32 * log2(N) bytes, while the Blockingtricia tree of Ethereum has 16 leaves per node, so the proof for these trees is 32 * 15 * log16(N) ~= 125 * log2(N) bytes). With around 250 million (~2²⁸) accounts in the state, the length of each proof is 125 * 28 = 3,500 bytes, or about 56,000 gas, plus the additional cost of decoding and verifying hashes.

Combining two proofs will cost around 100,000 to 150,000 gas (not including signature verification if used for each transaction), much more than the current basic 21,000 gas per transaction. However, if the proofs are verified on L2, the gap will be much wider. Computation on L2 is cheap because it is done off-chain and in an ecosystem with much fewer nodes than L1. On the other hand, data must be published to L1. So, it is not a comparison of 21,000 gas vs. 150,000 gas; it is a comparison of 21,000 L2 gas vs. 100,000 L1 gas.

We can calculate what this means by looking at the comparison between L1 gas costs and L2 gas costs:

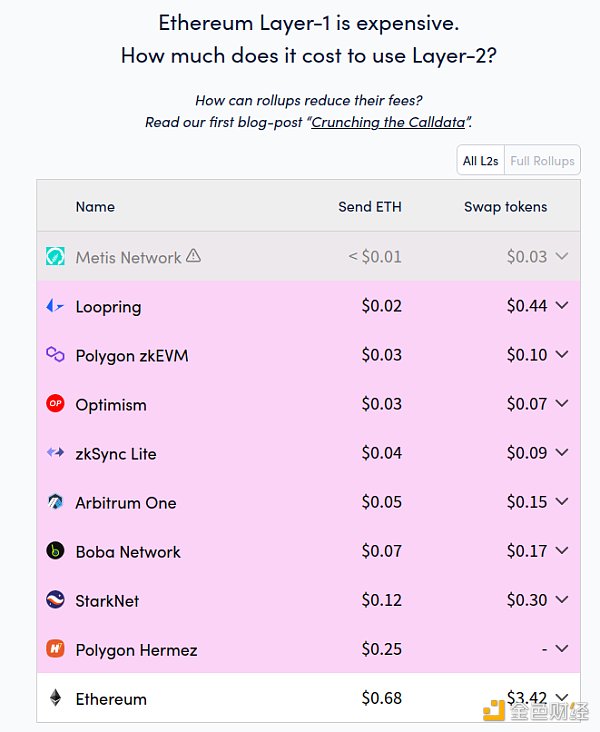L1’s simple send operation is currently 15-25 times more expensive than L2, and token exchange on L1 is 20-50 times more expensive than L2. Simple send operations are relatively heavy compared to data, but exchange operations are heavier in computation. Therefore, exchange operations are a better benchmark for approximating the cost comparison between L1 and L2 computation. Taking all these factors into account, if we assume a cost ratio of 30:1 between L1 computation cost and L2 computation cost, this seems to imply that placing a Merkle proof on L2 will be equivalent to approximately 50 regular transactions.

Of course, using binary Merkle trees can reduce the cost by about 4 times, but even so, the cost is likely to still be too high in most cases – we may need to look for better options if we are willing to no longer be compatible with Ethereum’s current decimal state tree.

How will ZK-SNARK proofs work?

In concept, ZK-SNARK proofs are pretty easy to understand, just replace the Merkle proofs in the above diagram with ZK-SNARK proofs that prove the existence of these Merkle proofs. The computational cost of a ZK-SNARK proof is around 400,000 gas and takes up about 400 bytes of data (compared to a basic transaction which has a computational cost of 21,000 gas and a data size of 100 bytes, which can be reduced to around 25 bytes with compression in the future). So, in terms of computation, the cost of ZK-SNARKs is 19 times the current basic transaction cost, and in terms of data, the cost of ZK-SNARKs is 4 times the basic transaction cost, and 16 times the future basic transaction cost.

Although these numbers are a significant improvement over Merkle proofs, they are still quite expensive. There are two ways to improve on this: (1) special-purpose KZG proofs or (2) aggregation, similar to ERC-4337 aggregation but using more complex math. We can explore both of these approaches.

How Does a KZG Proof for Special-Purpose Work?

First, let’s review how a KZG commitment works:

• We can use a KZG proof to represent a set of data [D₁…Dₙ], which is a proof of a polynomial P derived from the data: specifically, the polynomial P satisfies P(w) = D₁, P(w²) = D₂…P(wⁿ) = Dₙ. Here, w is a “unit root” that satisfies wᴺ = 1, where N is the size of the “evaluation domain” (all operations are performed in a finite field).

• To “commit” to P, we create an elliptic curve point com(P) = P₀ * G + P₁ * S₁ +…+ Pₖ * Sₖ. Here:

• G is the generator point of the curve.

• Pᵢ is the i-th coefficient of polynomial P.

• Sᵢ is the i-th point in the “trusted setup”.

• To prove P(z) = a, we create a “quotient polynomial” Q = (P – a) / (X – z), and create a commitment com(Q) to it. Such a polynomial can only be created if P(z) actually equals a.

• To verify a proof, we check the equation Q * (X – z) = P – a, and by performing an elliptic curve check on the proof com(Q) and polynomial commitment com(P), we check that e(com(Q), com(X – z)) ?= e(com(P) – com(a), com(1)).

Some important properties to understand:

• A proof is just the value of com(Q), which takes up 48 bytes.

• com(P₁) + com(P₂) = com(P₁ + P₂).

• This also means you can “edit” a value into an existing commitment. Suppose we know that Dᵢ is currently set to a, and we want to set it to b, and the existing commitment is com(P). Then, for the commitment “to P, but with P(wⁱ) = b and all other evaluations unchanged,” we set com(new_P) = com(P) + (b – a) * com(Lᵢ), where Lᵢ is a “Lagrange polynomial” that equals 1 at wⁱ and 0 at other wʲ points.

• To efficiently perform these updates, each client can precompute and store all N Lagrange polynomials (com(Lᵢ)). In the on-chain contract, storing all N commitments may be too much, so KZG commitments can be used instead by committing to the set of com(Lᵢ) (or the hash value of com(Lᵢ)), so that whenever someone needs to update the tree on-chain, they only need to provide the appropriate com(Lᵢ) and a proof of its correctness.

Therefore, we have a structure where we can keep adding values to the end of a growing list, albeit with some size limitations (in practice, possibly in the billions). We then use this as our commitment to manage (i) the key list stored on each L2 (com(key list)) and mirrored to L1, as well as (ii) the commitment data structure for the list of L2 keys stored on Ethereum L1.

Keeping the commitments updated may become part of the core L2 logic, or it may be achieved via deposit and withdrawal bridging without core L2 protocol changes.

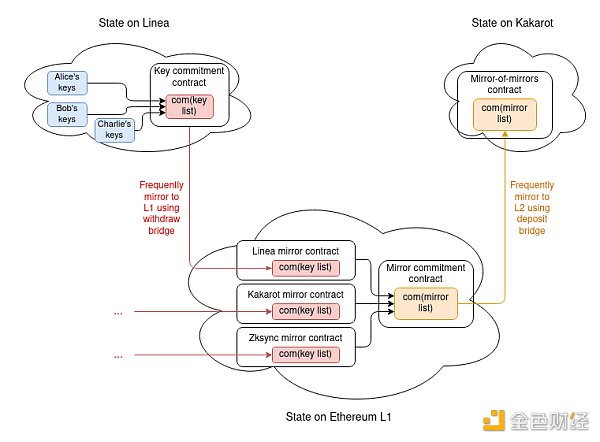The complete proof requires:

• The latest com(key list) on L2 holding the key store (48 bytes)

• The KZG proof of com(key list) in the com(mirror_list) storing all key list commitments (48 bytes)

• Your KZG proof of the key in com(key list) (48 bytes plus 4 bytes for the index)

• Actually, the two KZG proofs can be merged into one, so the total size is only 100 bytes.

Note one detail: since the key key list is a list, rather than a key/value map like the state, the key list will have to have positions assigned in order. The key commitment contract will have its own internal registry that maps each key store to an ID, and for each key, it will store hash(key, address of the key store), not just key, to unambiguously convey to other L2s which key store an entry is about.

The advantage of this technique is that it performs very well on L2. The data size is 100 bytes, about 4x smaller than ZK-SNARKs and much smaller than Merkle proofs. The computational cost is primarily one pairing check of size 2, which is about 119,000 gas. On L1, where data is not as important as computation, unfortunately KZG is somewhat more expensive than Merkle proofs.

How will Verkle trees work?

Verkle trees essentially involve stacking KZG commitments (or IBlocking commitments, which are more efficient and use simpler cryptography) on top of each other: to store 2⁴⁸ values, you can make a KZG commitment to a list of 2²⁴ values, each of which is itself a KZG commitment to 2²⁴ values. Verkle trees are being strongly considered for the Ethereum state tree, because Verkle trees can be used to store key-value maps, not just lists (basically, you can create a tree of size 2²⁵⁶ that is initially empty, and only fill in specific parts of the tree as needed).

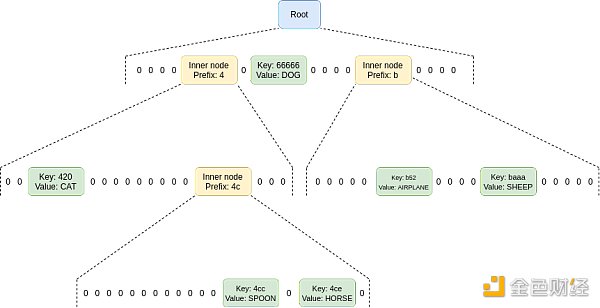The shape of a Verkle tree.

The proof of a Verkle tree is slightly longer than a KZG proof; they can be several hundred bytes long. They are also difficult to verify, especially if attempting to aggregate many proofs into one.

In fact, Verkle trees should be viewed as similar to Merkle trees, but with higher feasibility for non-SNARKing (due to lower data cost), and cheaper when using SNARKing (due to lower prover cost).

The biggest advantage of Verkle trees is their uniformity of data structure: Verkle proofs can be used directly on L1 or L2 states without covering structures, and use the same mechanism for both L1 and L2. Once quantum computers become a problem or once proving Merkle branches becomes efficient enough, Verkle trees can be swapped in place for binary hash trees using a hash function suitable for SNARKs.

Aggregation

If N users conduct N transactions (or, more realistically, N ERC-4337 UserOperations), N cross-chain declarations need to be proven. We can save a lot of gas by aggregating these proofs: Combining these transactions into a builder that enters the block or is packed into a block can create a single proof that proves all of these declarations at once.

This could mean:

• N Merkle branches of ZK-SNARK proofs

• KZG multiple proofs

• Verkle multiple proofs (or Verkle multiple proofs of ZK-SNARK)

In all three cases, the cost of each proof is only several hundred thousand gas. A builder needs to make such a proof for each user in L2 who uses the block; therefore, for the scheme to be useful to builders, it needs to have sufficient usage to typically have several transactions in the same block on multiple major L2s.

If using ZK-SNARKs, the main marginal cost is just the “business logic” of passing numbers between contracts, so each user may need a few thousand L2 gas. If using KZG multiple proofs, the prover needs to add 48 gas for each keystore-holding L2 containing L2, so the scheme’s marginal cost per user will increase by about 800 L1 gas on top of this (rather than per user). However, these costs are much lower than the cost of not aggregating, which inevitably involves more than 10,000 L1 gas and hundreds of thousands of L2 gas per user. For Verkle trees, you can use Verkle multiple proofs directly, adding about 100-200 bytes per user, or you can create a Verkle multiple proof of ZK-SNARK, whose cost is similar to that of a Merkle branch of ZK-SNARK, but the proof cost is much lower.

From an implementation perspective, it is best to aggregate cross-chain proofs through custom means by abstracting accounts through the ERC-4337 account standard. ERC-4337 has provided a mechanism for builders to aggregate UserOperations. There is even an implementation for BLS signature aggregation, which can reduce gas costs on L2 by 1.5x to 3x, depending on what other forms of compression are included.

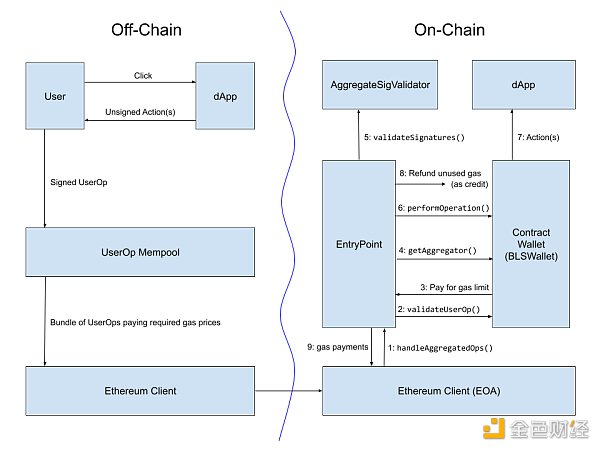Early version of the ERC-4337 BLS aggregation signature workflow

Direct state reading

The last possibility, applicable only to L2 reading L1 (not L1 reading L2), is to modify L2 to allow for direct static calls to contracts on L1.

This can be achieved through an opcode or precompile that allows for calling an address, gas, and calldata in L1 and returning an output, although since these calls are static, they cannot actually change any L1 state. L2 is already aware that L1 handles deposits, so there is technically no fundamental reason why this mechanism cannot be implemented (see: Optimism provides RFP support for static calls into L1).

Note that if the keystore is on L1 and L2 integrates L1 static call functionality, then no proofs are necessary! However, if L2 does not integrate L1 static calls, or if the keystore is on L2 (which may happen once L1 becomes too expensive to use even for slightly active users), then proofs will be necessary.

How L2 obtains the latest Ethereum state root

To handle messages from L1 to L2 (especially deposits), all L2s need some mechanism for accessing the latest L1 state. In fact, if an L2 has deposit functionality, you can move the L1 state root to the L2 as-is: simply have a contract on L1 call the BLOCKHASH opcode and pass it as a deposit message to the L2. The L2 end can receive the full block header and extract its state root. However, each L2 is best served by having a clear way to directly access the latest comprehensive L1 state or the most recent L1 state root.

The main challenge in optimizing L2’s receipt of the latest L1 state root is to simultaneously achieve security and low latency:

• If L2 implements “direct L1 reads” in a delayed fashion, only reading finalized L1 state roots, the delay is typically 15 minutes, but in extreme cases, such as inactive leaks (which must be tolerable), the delay can be as long as several weeks.

• L2 can indeed be designed to read more recent L1 state roots, but because L1 may experience rollbacks (even in the case of single-slot finality, rollbacks can occur during inactive leak periods), L2 also needs to be able to roll back. From a software engineering perspective, this is technically challenging, but at least Optimism has already demonstrated this capability.

• If using a deposit bridge to bring L1 state roots into L2, simple economic viability may require longer intervals between deposit updates: if the entire cost of a deposit is 100,000 gas, and assuming an ETH price of $1,800 and a fee of 200 Gwei, updating the L1 state root to L2 once per day would cost each L2 $36 per day, or $13,148 per L2 per year, to maintain the system. If the delay is one hour, this cost will increase to $315,569 per L2 per year. In the best case, some wealthy users eager to pay for updates will pay, keeping the system up-to-date to service other users. In the worst case, some altruistic participant will have to pay the cost themselves.

• “Oracles” (known as “prophets” to at least some DeFi enthusiasts) are not an acceptable solution here: wallet key management is a very critical foundational function, so it should depend on some very simple, cryptographically trusted foundational infrastructure at most.

Additionally, in reverse (L1 reads L2):

• In optimistic rollups, it takes a week for the state root to reach L1 due to fraud proof delays. In zero-knowledge rollups, it currently takes several hours due to the combination of proof time and economic constraints, but future technology will reduce this time.

• In the case of L1 reading L2, “pre-confirmation” (from sorters, certifiers, etc.) is not an acceptable solution. Wallet management is a very critical security low-level function, so the security level of L2->L1 communication must be absolute: it is even impossible to push an incorrect L1 state root by taking over the L2 validator set. The only state root that L1 should trust is the state root held by the L2 on L1 that the contract has accepted as final.

The speed of some cross-chain operations is too slow for many DeFi use cases; for these cases, we do need faster bridging solutions, but the security model of these solutions may not be sufficient. However, for use cases where wallet key updates are concerned, the longer delay is more acceptable: you are not delaying transactions by a few hours, but rather delaying key changes. You only need to keep the old key for a longer period of time. If the reason for changing the key is because the key has been stolen, you will face a fairly long vulnerability period, but you can mitigate the risk with some measures, such as freezing the wallet.

Overall, the best solution to minimize latency is for L2 to be able to directly read the L1 state (or at least the state root) in the best possible way, with each L2 block (or state root calculation log) containing a pointer to the nearest L1 block, so that if L1 rolls back, L2 can also roll back. The key library contract should be placed on the mainnet or ZK rollup L2, so that it can be quickly submitted to L1.

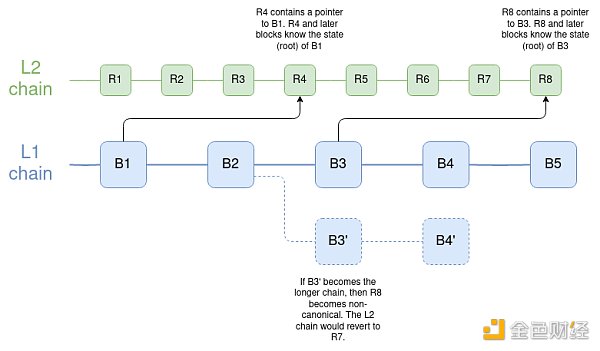
How many connections do other chains need to maintain wallets based on Ethereum or L2 roots?

Surprisingly, this connection does not need to be too many. It doesn’t even need to be a formal L2, if it is an L3 or validium, as long as the chain has direct access to the Ethereum state root and technical and social commitments to reorganize or hard fork when Ethereum rolls back.

An interesting research question is to determine to what extent a chain is connected to multiple other chains (such as Ethereum and Zcash) in this form of connection. A direct and naive approach is possible, that is, if Ethereum or Zcash rolls back, the dense chain will have to be reorganized (and hard forked when Ethereum or Zcash hard forks), but then your community will have double technical and political dependencies (or more dependencies if your chain is bound to many other chains). The scheme based on ZK bridging is not robust against 51% attacks or hard forks. There may be smarter solutions.

Privacy Protection

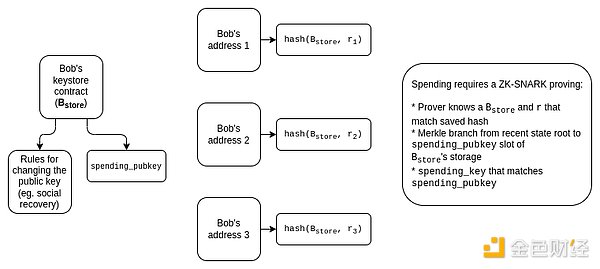
Ideally, we also want to protect privacy. If you have many wallets managed by the same key store, we want to ensure that:

• The public does not know that these wallets are related to each other.

• Social recovery guardians do not know what addresses they are guarding.

This raises some issues:

• We cannot directly use Merkle proofs because they cannot protect privacy.

• If we use KZG or SNARKs, then the proof needs to provide a blinded version of the verification key without leaking the position of the verification key.

• If we use aggregation, then the aggregator should not know the position in plaintext; instead, the aggregator should receive blinded proofs and have a way to aggregate them.

• We cannot use a “lightweight version” (updating the key using only cross-chain proofs) because it leaks privacy: if multiple wallets are updated simultaneously due to the update process, the temporal leak will imply that these wallets may be related. Therefore, we must use a “heavyweight version” (using cross-chain proofs for each transaction).

For SNARKs, the solution is conceptually simple: the proof defaults to hidden information, and the aggregator needs to generate recursive SNARKs to prove these SNARKs.

The main challenge of this approach is that aggregation requires the aggregator to create recursive SNARKs, which is relatively slow in the current situation.

For KZG, we can start with the work of non-index leakage KZG proof (also see the more formal version of this work in the Caulk paper). However, the aggregation of blinded proofs is an open problem that requires more attention.

Unfortunately, directly reading L1 from within L2 does not provide privacy protection, although implementing direct reading is still very useful, both to minimize latency and for other applications.

Summary

• The most realistic workflow to implement cross-chain social recovery wallets is to maintain a keystore in one place and maintain multiple wallets in many locations, where the wallets either (i) read the keystore to update their local authenticated key view, or (ii) read the keystore on every transaction verification.

• A key factor in achieving this goal is cross-chain proof. We need to work hard to optimize these proofs. The best choice may be ZK-SNARKs, Verkle proofs, which are waiting to emerge, or self-built KZG solutions.

• In the long run, aggregation protocols will be necessary, and aggregators will generate aggregate proofs as part of creating bundles of all UserOperations submitted by users to minimize costs. This may need to be integrated with the ERC-4337 ecosystem, although some modifications to ERC-4337 may be necessary.

• L2 should be optimized to minimize the latency of reading L1 status (or at least the status root) from within L2. Directly reading L1 status from L2 is ideal and can save proof space.

• Wallets can be deployed not only on L2, but also on systems that are lower connected to Ethereum (L3, or even agree to include only the Ethereum state root and reorganize or hard fork independently of Ethereum when rolling back or hard forking).

• However, the keystore should be placed on L1 or a highly secure ZK rollup L2. Placing the keystore on L1 can save a lot of complexity, although in the long run, even this may be too expensive, so the keystore needs to be placed on L2.

• Protecting privacy will require additional work and add some difficulty. However, we should move towards privacy-preserving solutions and ensure that any solutions we propose remain forward-compatible with privacy protection.

We will continue to update Blocking; if you have any questions or suggestions, please contact us!