a16z Why It’s Said that Stateless Blockchain Cannot Exist

a16z on the Infeasibility of Stateless Blockchains

Author: MirandaChrist (Ph.D. student in Computer Science at Columbia University/a16z Crypto Research Intern), JosephBonneau (a16zcrypto) Source: a16z crypto; Translation: Yvonne, MarsBit

As blockchain supports more users and more frequent transactions, the amount of information (“state”) stored by validators to verify transactions is also increasing. For example, in Bitcoin, the state consists of a set of unspent transaction outputs (UTXOs). In Ethereum, the state consists of the account balances for each account and the code and storage for each smart contract.

For blockchains that have enough accounts or UTXOs to support the majority of people’s daily transactions, this storage burden will become difficult to handle, making it challenging for them to become validators and pose a threat to decentralization. It is easy to use cryptography as a solution, and tools like Merkle trees and zero-knowledge proofs have helped us achieve goals that were previously unimaginable.

This is exactly the goal of “stateless blockchains”. However, despite a lot of work in this area, they are still far from practical. But it has been proven that this lag in progress is inherent – the gap between these structures and practicality can never be bridged. Our recent work shows that any stateless blockchain solution, no matter how intelligent, is impractical without additional measures to manage the state. As we will demonstrate at the end of this article, this impossible outcome should not be discouraging.

• a16z Research on the Impossibility of Stateless Blockchain
• a16z Crypto Partner discusses NFT Royalties How it Works, Evolution, and Solutions
• Why is data availability sampling important for blockchain scalability?

Stateless State

Today, the scale of the state is large but manageable. For example, Bitcoin nodes store about 7GB of data, and Ethereum nodes store about 650GB of data. However, the storage burden of full nodes grows roughly linearly with the throughput of the chain (transactions per second or TPS), and the current throughput is too low to be acceptable. Based on current design, the state required to truly support daily transactions (hundreds of thousands to millions of TPS) will become difficult to handle, requiring several TB or even PB of storage space.

This has prompted people to seek technical methods to significantly reduce the amount of state required by validators – stateless blockchains, which would require validators to store only a constant-sized state regardless of the transaction throughput. (In fact, this term is a misnomer: there is still state, but it is small enough to accommodate any future throughput – typically a constant size.) This lightweight storage requirement will make it easier to run validator nodes; optimistically, everyone can run a node on their phone. It is important to lower the barrier of entry for validators because increasing the number of validators will increase the security of the chain.

Despite extensive research on stateless blockchains (e.g., Todd, Buterin, Boneh, Srinivasan, etc.), they are far from practical and, to our knowledge, none have been deployed. The fundamental problem with all known stateless blockchains is that they require users to store additional data called witnesses to help validators verify transactions involving their accounts. For example, this witness could be a Merkle proof showing that the user’s account and its balance are included in the global state commitment. When users make transactions, they submit this witness to validators to demonstrate that their account has sufficient balance.

Unlike private keys that never need to be changed, these witnesses often change, even for users who are not actively trading, which imposes an unrealistic burden on users. Similarly, imagine if you had to continuously monitor all other credit card transactions worldwide and update some local data accordingly in order to use your own credit card. In order to make blockchain practical, users must be able to stay offline and only interact with the blockchain when submitting transactions. In many cases, such as hardware wallets, updating witnesses is not only inconvenient but also impossible.

This leads to a natural research question: Can we build a stateless blockchain that does not require updating witnesses (or requires minimal witness updates)? To answer this question, we have developed a new theoretical framework (reversible proof systems) that encompasses stateless blockchains. Using this framework, we have proven a conclusive impossibility result: the trade-off between concise global state and frequent witness updates is fundamental. Our proof technique is information-theoretic, which means that future computers will not be powerful enough to solve this problem: the gap between stateless blockchain structure and practicality will remain unbridgeable.

Research Background

To help build intuition for the impossibility result, we will first describe the natural but inefficient construction of a stateless blockchain using Merkle trees. Our goal is to allow validators to determine if the transactions submitted by users are valid—for example, if the user has a sufficiently large account balance to carry out the transaction. In a stateless blockchain scheme, validators store a constant-sized state. When users make transactions, they must include a witness in the transaction. Validators can use the current state and the (transaction, witness) pair submitted by the user to verify if the user has enough account balance to carry out the transaction.

We first construct a Merkle tree where each (account ID, balance) pair (a, b) is included as a leaf. The constant-sized state V stored by validators is the root of this tree, serving as a commitment to the set of account balance pairs. Each user maintains a Merkle inclusion proof for their (account ID, balance) pair as their witness. The Merkle inclusion proof for leaf (a, b) consists of the sibling nodes (v1, …, vk) along the path from the leaf to the root of the tree. Given a transaction performed by a user using account a and claiming balance b, the validator can check if b is indeed the balance of account a by verifying the proof (v1, …, vk) for (a, b) against their current state V. If so, the validator will execute the transaction and must update the account balance accordingly. One convenient property of Merkle trees is that given the Merkle inclusion proof for a leaf, it is easy to compute the resulting root when that leaf changes. In other words, validators can easily compute the updated state V’ that captures the new balance of account a after the transaction is executed.

The Merkle tree scheme has two main drawbacks. First, the number of witnesses for users is relatively large and grows logarithmically with the total number of accounts in the system. Ideally, they should be of constant size, which can be achieved using schemes like RSA accumulators (studied by Boneh et al. in the context of stateless blockchains).

The second disadvantage is more difficult to avoid: whenever other users make transactions, the proof of the account-balance pair will change. Remember, the proof of a leaf consists of the companion nodes (LianGuairtner nodes) on the path from that leaf to the root of the tree. If any other leaf changes, one of these nodes will also change, causing practical problems. Most blockchain users want to passively store their tokens in a wallet and only log in when they want to make a transaction. However, in the practice of this stateless blockchain, users must constantly monitor the transactions of others to keep their proofs up to date. (Although third parties can monitor on behalf of users, this deviates from the standard stateless blockchain model. We will discuss this issue at the end of this article.) In fact, this is an insurmountable challenge for stateless blockchains, burdening users heavily.

Our conclusion: Stateless is impossible

This phenomenon is not unique to the Merkle tree structure – all known stateless blockchain schemes require users to update their proofs frequently. We have demonstrated this in this article. More precisely, we have shown that the number of users who must update their proofs roughly increases linearly with the total number of transactions performed by all users.

This means that even if the user Alice does not make any transactions, her proof may need to be changed as other users make transactions. As long as the compact state stored by the validator is too small to capture the complete state (i.e., the collection of all account balances), increasing the size of the compact state is not helpful. We have plotted this relationship according to the following theorem, as well as the number of proof changes required per day for blockchains with different throughput. These graphs show the number of proof changes required for optimal stateless blockchains. Here, the data domain refers to the total number of accounts (in the account model) or UTXOs (in the UTXO model).

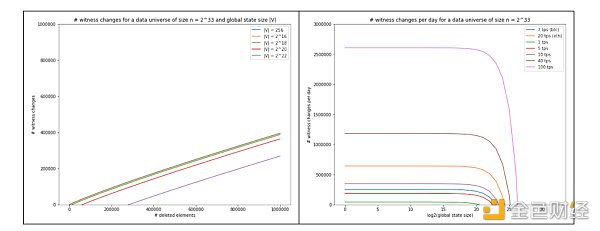
The core of our proof is an information-theoretical argument. One of the core principles of information theory proposed by Claude Shannon is that if Alice randomly selects an object from a set of size 2n and wants to tell Bob which object she chose, she must send him at least n bits. If there exists a stateless blockchain scheme where users rarely update their proofs, then Alice can tell Bob which object she chose in less than n bits of time – Shannon proved that this is impossible. Therefore, such a stateless blockchain is impossible.

For simplicity, we will describe a slightly weaker statement here: it is impossible for a stateless blockchain to exist where users never need to update their proofs. The key idea is that Alice uses a stateless blockchain scheme to encode her message to Bob. Initially, Alice and Bob both know the complete account balance pairs for all n users. Assume that each account has at least one coin. Alice and Bob also know the compact state V of the stateless blockchain and the witnesses w_i for all account balance pairs (a_i, b_i). Alice and Bob have also reached an agreement on the mapping between messages and sets of accounts. Alice will choose a set of accounts A corresponding to her message, and then she will spend tokens from these accounts. She will use the stateless blockchain to communicate with Bob the set she chose, and he can learn what her message is from this set.

Encoding: Alice spends one token from each account of A. Using a stateless blockchain scheme, Alice calculates the updated state V’ and sends V’ to Bob.

Decoding: For each i, Bob checks if Verify(wi, (ai, bi)). Bob outputs a set of accounts B, such that Verify(wi, (ai, bi)) = false.

Bob successfully outputs the same set as Alice selected: B = A. First, observe that if Alice spends a token from account ai, the witness of its old balance should no longer be accepted – otherwise, Alice would be able to double spend. Therefore, for each account ai in A, Verify(wi, (ai, bi)) = false, and Bob includes that account in B. On the other hand, Bob never includes an account identified by Alice in B. No token is spent on these accounts as their balances remain unchanged, and their witnesses (remember the loose statement we aim to prove) never change. Therefore, B is exactly equal to A.

Finally, the contradiction is resolved by calculating the number of bits Alice should send to Bob. There are 2n possible subsets of accounts she can choose, and according to Shannon’s theorem, she should send at least n bits to Bob. However, she only sends a constant-sized state V’, which is much shorter than n bits.

(Readers familiar with cryptography may notice that we are omitting some details here; for example, the probability of Bob’s decoding failure can be ignored. Our paper includes a complete proof.)

Although we describe our proof using a stateless blockchain, Alice and Bob can use various other authenticated data structures (such as accumulators, vector commitments) to perform similarly efficient communication. We use a new abstraction to formalize such data structures, which we call revocable proof systems.

Implications of the Result

Our result shows that you cannot “encrypt the state” – there is no magic solution that allows us to build a stateless blockchain where users never have to update their witnesses. The state does not disappear but rather shifts from validators to users, pushed to users in the form of frequent witness updates.

Indeed, there are some potential solutions, but these solutions depart from the strict stateless blockchain model. The model allows a third party (neither a user nor a validator) to be responsible for storing the complete state. This party is called the proof-of-service node (studied most rigorously by Srinivasan et al.), which uses the complete state to generate the latest witnesses on behalf of users. Users can then use these witnesses to transact, just like in a regular stateless blockchain where validators still only store a concise state. The incentive mechanisms of this system, particularly how users compensate proof-of-service nodes, are an interesting open research direction.

While our discussion so far has focused mainly on L1 blockchains, our results also have implications for L2 systems such as rollup servers. Rollups (whether optimistic or ZK) typically use a large state and submit it with a small value stored on L1. This state includes the accounts of each user on L2. We hope that these users can directly withdraw funds on L1 by publishing witness of their current account balances, without the cooperation of L2 servers. This setup is also an instance of the revocable proof system in our model. In fact, one could argue that stateless blockchains have already been implemented in practice in the form of L2 rollups.

Unfortunately, this means that our infeasibility result directly applies. User rollup withdrawals witnesses must be frequently changed, otherwise almost the entire L2 state must be written to L1. Therefore, today’s aggregators typically assume the existence of a data availability committee (sometimes called “validity committee”), which functions similarly to “proof-of-service” nodes, helping users compute new witnesses when they are ready to exit. Our research findings suggest that the warning in the Ethereum documentation to users – “If transaction data is not accessible, users cannot compute the Merkle proof necessary to prove ownership of funds and execute a withdrawal.” – will always hold true.

As blockchain systems evolve, it becomes increasingly important to develop more efficient methods for managing blockchain states. Although our exclusion of stateless blockchains may seem negative, infeasibility results are useful for blockchain designers because they tell us to focus our research efforts elsewhere, ideally helping us find viable solutions faster.

We will continue to update Blocking; if you have any questions or suggestions, please contact us!